
题目列表(包括答案和解析)
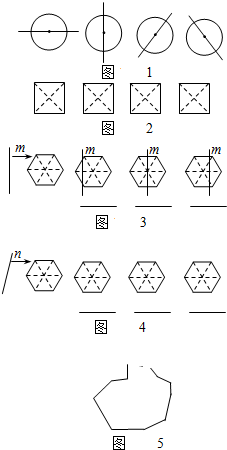 (2013•池州一模)我们知道:由于圆是中心对称图形,所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分(如图1).
(2013•池州一模)我们知道:由于圆是中心对称图形,所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分(如图1).
 17、为了增加游人观赏花园风景的路程,将平行四边形花园中形如图1的恒宽为a米的直路改为形如图2恒宽为a米的曲路,道路改造前后各余下的面积(即图中阴影部分面积)分别记为S1和S2,则S1
17、为了增加游人观赏花园风景的路程,将平行四边形花园中形如图1的恒宽为a米的直路改为形如图2恒宽为a米的曲路,道路改造前后各余下的面积(即图中阴影部分面积)分别记为S1和S2,则S1 如图,Rt△ABC中,∠ACB=90°.在AB的同侧分别以AB、BC、AC为直径作三个半圆.图中阴影部分的面积分别记作为S1和S2.
如图,Rt△ABC中,∠ACB=90°.在AB的同侧分别以AB、BC、AC为直径作三个半圆.图中阴影部分的面积分别记作为S1和S2.| 6 |
为了增加游人观赏花园风景的路程, 将平行四边形花园中形如图1的恒宽为a米的直路改为形如图2恒宽为a米的曲路, 道路改造前后各余下的面积
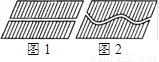
(即图中阴影部分面积)分别记为S1和S2,则S1________S2(填“>”“=”或“<”).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com