
题目列表(包括答案和解析)
如图,⊙O的弦AB、CD相交于点P,PA=4厘米,PB=3厘米,PC=6厘米,EA切⊙O于点A,AE与CD的延长线交于点E,AE=2![]() 厘米,则PE的长为( )
厘米,则PE的长为( )
(A)4厘米 (B)3厘米 (C)![]() 厘米 (D)
厘米 (D)![]() 厘米
厘米
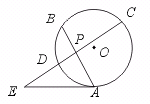
如图,⊙O中,两条弦AB、CD相交于P点,若PA=4,PB=3,PC=6,则CD的长为__________.

如图所示,⊙O的两条弦AB、CD相交于点E,AC和DB的延长线交于点P,则下列结论中成立的是

[ ]
A.PC·CA=PB·BD
B.CE·AE=BE·ED
C.CE·CD=BE·BA
D.PB·PD=PC·PA
.(9分)如图,AB为⊙O内垂直于直径的弦,AB、CD相于点H,△AED与△AHD
关于直线AD成轴对称.
(1)试说明:AE为⊙O的切线;
(2)延长AE与CD交于点P,已知PA=2,PD=1,求⊙O的半径和DE的长.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com