某班同学“五•一”期间组织外出爬山活动,花了230元租了一辆客车,如果参加活动的同学每人交7元租车费还不够,你明白这句话的含义吗?
典例分析:
例1在公路上,我们可以看到以下几种交通标志(如图),它们有着不同的意义.如果设汽车载重量为x吨,宽度为k米,高度为h米,速度为y千米/时,请你用不等式表示下列各种标志的意义.
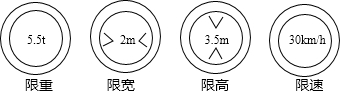
思路分析:由题意可知,限重、限宽、限高、限速中的“限”字的意义就是不超过,也就是“≤”的意义.这样,该题即可迎刃而解.
解:x≤5.5 k≤2 h≤3.5 y≤30
方法点拨:生活中的各种标志图、徽标等信息,现已成为考试中的一种素材,解决这类题目,需要将信息转化为数学语言,比如将“大于”“超过”“不超过”“非负数”“不大于”等等,准确“翻译”为数学符号.通过本题可以使我们认识到关注身边的数学的重要性.
例2用适当的不等式表示下列关系:
(1)x的4倍与2的和是非负数,可表示为
.
(2)育才中学七年级一班学生数不到35人,设该班学生有x人,可表示为
.
(3)人的寿命可超过120岁.设人的寿命为x岁,则可表示为
.
(4)小林家有4口人,人均住房面积不足15平方米,则小林家的总住面积y平方米可表示为
.
思路分析:(1)中的“非负数”即“≥0”的数;(2)中的“不到”即“<”的意思;(3)中的“超过”即“>”的意思;(4)中的“不足”即“<”的意思.
答案:(1)4x+2≥0 (2)x<35 (3)x>120 (4)y<60
方法点拨:做这种类型的题时,要善于把实际问题中的一些“不到”“大于”“超过”“不小于”等数学术语,准确迅速地转化为数学符号.此类题是为学生以后列不等式解应用题做铺垫的,所以必须掌握好.