
题目列表(包括答案和解析)
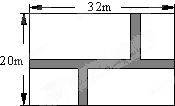 如图,某小区在宽20m,长32m的矩形地面上修筑同样宽的人行道(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m2,求道路的宽.设道路宽是x,则列方程为
如图,某小区在宽20m,长32m的矩形地面上修筑同样宽的人行道(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m2,求道路的宽.设道路宽是x,则列方程为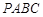 的边长为1,将其沿
的边长为1,将其沿 轴的正方向连续滚动,即先以顶点A为旋转中心将正方形
轴的正方向连续滚动,即先以顶点A为旋转中心将正方形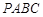 顺时针旋转90°得到第二个正方形,再以顶点D为旋转中心将第二个正方形顺时针旋转90°得到第三个正方形,依此方法继续滚动下去得到第四个正方形,…,第n个正方形.设滚动过程中的点P的坐标为
顺时针旋转90°得到第二个正方形,再以顶点D为旋转中心将第二个正方形顺时针旋转90°得到第三个正方形,依此方法继续滚动下去得到第四个正方形,…,第n个正方形.设滚动过程中的点P的坐标为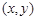 .
.
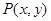 运动的曲线(0≤
运动的曲线(0≤ ≤4),并直接写出该曲线与
≤4),并直接写出该曲线与 轴所围成区域的面积.
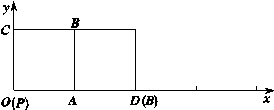
轴所围成区域的面积.如图所示,在平面直角坐标系xOy中,正方形 的边长为1,将其沿
的边长为1,将其沿 轴的正方向连续滚动,即先以顶点A为旋转中心将正方形
轴的正方向连续滚动,即先以顶点A为旋转中心将正方形 顺时针旋转90°得到第二个正方形,再以顶点D为旋转中心将第二个正方形顺时针旋转90°得到第三个正方形,依此方法继续滚动下去得到第四个正方形,…,第n个正方形.设滚动过程中的点P的坐标为
顺时针旋转90°得到第二个正方形,再以顶点D为旋转中心将第二个正方形顺时针旋转90°得到第三个正方形,依此方法继续滚动下去得到第四个正方形,…,第n个正方形.设滚动过程中的点P的坐标为 .
.
【小题1】(1)画出第三个和第四个正方形的位置,并直接写出第三个正方形中的点P的坐标;
【小题2】(2)画出点 运动的曲线(0≤
运动的曲线(0≤ ≤4),并直接写出该曲线与
≤4),并直接写出该曲线与 轴所围成区域的面积.
轴所围成区域的面积.
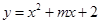 的图象与
的图象与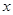 轴的正半轴交于点
轴的正半轴交于点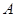 ,与
,与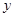 轴的正半轴交交于点
轴的正半轴交交于点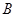 ,且
,且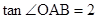 .设此二次函数图象的顶点为
.设此二次函数图象的顶点为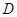 。
。
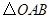 绕点
绕点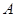 顺时针旋转
顺时针旋转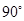 后,点
后,点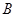 落到点
落到点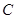 的位置.将上述二次函数图象沿
的位置.将上述二次函数图象沿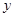 轴向上或向下平移后经过点
轴向上或向下平移后经过点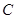 .请直接写出点
.请直接写出点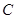 的坐标和平移后所得图象的函数解析式;
的坐标和平移后所得图象的函数解析式;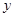 轴的交点为
轴的交点为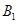 ,顶点为
,顶点为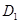 .点
.点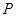 在平移后的二次函数图象上,且满足
在平移后的二次函数图象上,且满足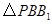 的面积是
的面积是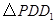 面积的
面积的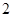 倍,求点
倍,求点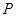 的坐标。
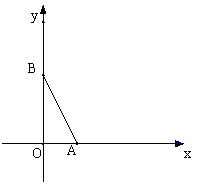
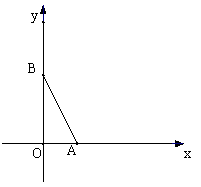
的坐标。如图,在直角坐标系中,O为坐标原点,二次函数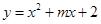 的图象与
的图象与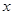 轴的正半轴交于点
轴的正半轴交于点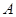 ,与
,与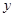 轴的正半轴交交于点
轴的正半轴交交于点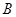 ,且
,且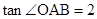 .设此二次函数图象的顶点为
.设此二次函数图象的顶点为 。
。
【小题1】(1)求这个二次函数的解析式;
【小题2】(2)将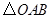 绕点
绕点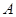 顺时针旋转
顺时针旋转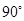 后,点
后,点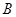 落到点
落到点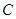 的位置.将上述二次函数图象沿
的位置.将上述二次函数图象沿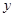 轴向上或向下平移后经过点
轴向上或向下平移后经过点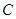 .请直接写出点
.请直接写出点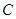 的坐标和平移后所得图象的函数解析式;
的坐标和平移后所得图象的函数解析式;
【小题3】(3)设(2)中平移后所得二次函数图象与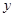 轴的交点为
轴的交点为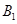 ,顶点为
,顶点为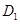 .点
.点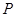 在平移后的二次函数图象上,且满足
在平移后的二次函数图象上,且满足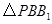 的面积是
的面积是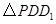 面积的
面积的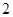 倍,求点
倍,求点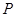 的坐标。
的坐标。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com