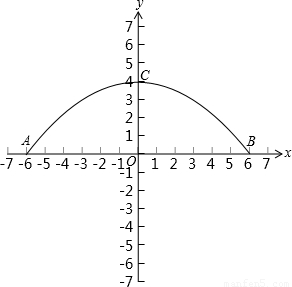
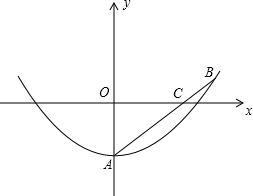
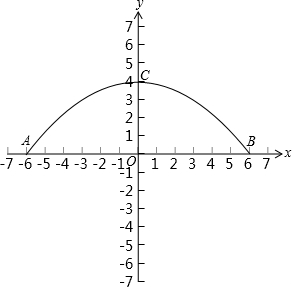
如图，有一个横截面是抛物线的运河，一次，运河管理员将一根长6m的钢管（AB）一端在运河底部A点，另一端露出水面并靠在运河边缘的B点，发现钢管4m浸没在水中（AC=4米），露出水面部分的钢管BC与水面部分的钢管BC与水面成30°的夹角（钢管与抛物线的横截面在同一平面内）
（1）以水面所在直线为x轴，建立如图所示的直角坐标系，求该运河横截面的抛物线解析式；
（2）若有一艘货船从当中通过，已知货船底部最宽处为12米，吃水深（即船底与水面的距离）为1米，此时货船是否能安全通过该运河？若能，请说明理由；若不能，则需上游开闸放水提高水位，当水位上升多少米时，货船能顺利通过运河？（船与河床之间的缝隙忽略不计）
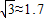