
题目列表(包括答案和解析)
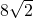 厘米,对角线AC上的两个动点E,F.点E从点A,点F从点C同时出发,沿对角线以1厘米/秒的相同速度运动,过E作EH⊥AC交Rt△ACD的直角边于H,过F作FG⊥AC交Rt△ACD的直角边于G,连接HG,EB.设HE、EF、FG、GH围成的图形面积为S1,AE,EB,BA围成的图形面积为S2(
厘米,对角线AC上的两个动点E,F.点E从点A,点F从点C同时出发,沿对角线以1厘米/秒的相同速度运动,过E作EH⊥AC交Rt△ACD的直角边于H,过F作FG⊥AC交Rt△ACD的直角边于G,连接HG,EB.设HE、EF、FG、GH围成的图形面积为S1,AE,EB,BA围成的图形面积为S2( 这里规定:线段的面积为0)E到达C,F到达A停止.若E的运动时间为x秒,解答下列问题:
这里规定:线段的面积为0)E到达C,F到达A停止.若E的运动时间为x秒,解答下列问题: 厘米,
厘米,
 厘米,解答下列问题(结果可用含
厘米,解答下列问题(结果可用含 ,
, 的代数式表示).
的代数式表示). 中,底面为菱形,
中,底面为菱形, ,
, 与底面
与底面 垂直,
垂直, ,
, 为棱
为棱 的中点,
的中点, 为
为 的中点,
的中点, 为
为 的交点,
的交点,
 ;
; 的余弦值.
的余弦值.阅读下列材料:
题目:已知实数a,x满足a>2且x>2,试判断 与
与 的大小关系,并加以说明.
的大小关系,并加以说明.
思路:可用“求差法”比较两个数的大小,先列出![]() 与
与![]() 的差
的差![]() ,再
,再
说明y的符号即可.
现给出如下利用函数解决问题的方法:
简解:可将y的代数式整理成![]() ,要判断y的符号可借助函数
,要判断y的符号可借助函数![]() 的图象和性质解决.
的图象和性质解决.
参考以上解题思路解决以下问题:
已知a,b,c都是非负数,a<5,且 ![]() ,
,![]() .
.
1.(1)分别用含a的代数式表示4b,4c;
2.(2)说明a,b,c之间的大小关系.
阅读下列材料:
题目:已知实数a,x满足a>2且x>2,试判断 与
与 的大小关系,并加以说明.
的大小关系,并加以说明.
思路:可用“求差法”比较两个数的大小,先列出 与
与 的差
的差 ,再
,再
说明y的符号即可.[来源:Z。xx。k.Com]
现给出如下利用函数解决问题的方法:
简解:可将y的代数式整理成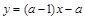 ,要判断y的符号可借助函数
,要判断y的符号可借助函数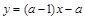 的图象和性质解决.
的图象和性质解决.
参考以上解题思路解决以下问题:
已知a,b,c都是非负数,a<5,且 ,
, .
.
【小题1】(1)分别用含a的代数式表示4b,4c;
【小题2】(2)说明a,b,c之间的大小关系.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com