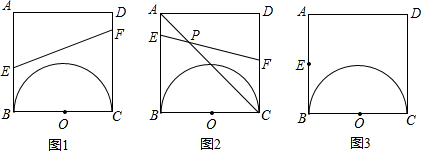
如图1，正方形ABCD中，有一直径为BC=2cm 的半圆O．两点E、F分别从点B、点A同时出发，点E沿线段BA以1cm/s的速度向点A运动，点F沿折线A-D-C以2cm/s的速度向点C运动．设点E离开点的B时间为t（s），其中1≤t＜2．
（1）当t为何值时，线段EF和BC平行？
（2）EF能否与半圆O相切？如果能，求出t的值；如果不能，请说明原因．
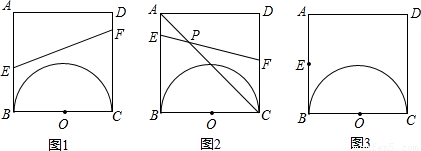
（3）如图2，设EF与AC相交于点P，当点E、F运动时，点P的位置是否发生变化？若发生变化，请说明理由；若不发生变化，也请说明理由，并求AP：PC的值．
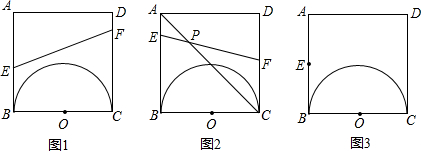
变式：如图3，若将上题改为，正方形ABCD中，有一直径为BC=2cm的半圆O．点E为AB边上的动点（不与点A、B重合），过点E与圆O相切的直线交CD所在直线为点F，设EB=x，FD=y．
（1）试写出y关于x的函数关系式，并写出自变量x的取值范围．
（2）是否存在切线EF，把正方形ABCD的周长分成相等的两部分？若存在，求出x的值．若不存在，请说明理由．