如图1，在△ABC中，E为对角线AB上一点，以AE为一边作正方形AEFH，点F在AC上，连接BF，G为BF中点，连接EG，CG．
（1）求证：EG=CG；
（2）将图1中正方形AEFH绕A点逆时针旋转45°，如图2所示，取BF中点G，连接EG，CG．问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；
（3）将图1中正方形AEFH绕B点旋转任意角度，如图3所示，再连接相应的线段，问（1）中的结论是否仍然成立？通过观察你还能得出什么结论？（均不要求证明）

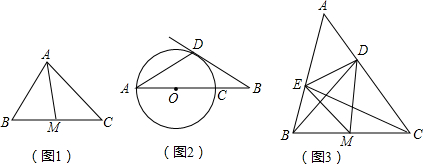
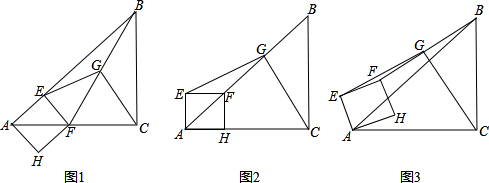
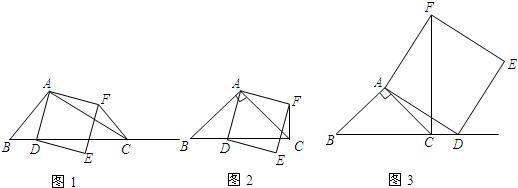
如图1，在△ABC中，∠ACB为锐角．点D为射线BC上一动点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．解答下列问题：
（1）如果AB=AC，∠BAC=90°．
①当点D在线段BC上时（与点B不重合），如图2，线段CF、BD之间的位置关系为，数量关系为；
②当点D在线段BC的延长线上时，如图3，①中的结论是否仍然成立，为什么？

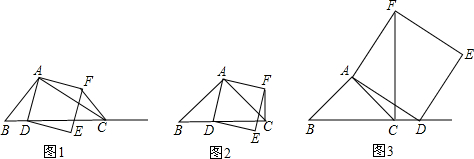
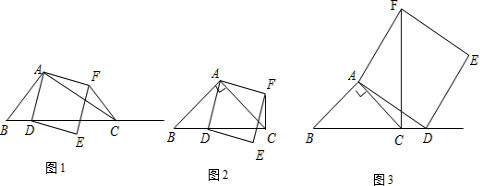
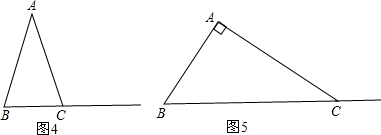
（2）①如果AB=AC，∠BAC≠90°，点D在射线BC上运动．在图4中同样作出正方形ADEF，你发现（1）问中的结论是否成立？不用说明理由；
②如果∠BAC=90°，AB≠AC，点D在射线BC上运动．在图5中同样作出正方形ADEF，你发现（1）问中的结论是否成立？不用说明理由；

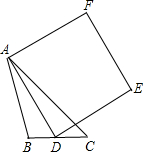
（3）要使（1）问中CF⊥BC的结论成立，试探究：△ABC应满足的一个条件，（点C、F重合除外）画出相应图形（画图不写作法），并说明理由；
（4）在（3）问的条件下，设正方形ADEF的边DE与线段CF相交于点P，设AC=2

2

，BC=

3

2

，求线段CP长的最大值．

如图1，在△ABC中，∠ACB为锐角，点D为射线BC上一点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．
解答下列问题：
（1）如果AB=AC，∠BAC=90°，点D在射线BC上运动时（与点B不重合），如图，线段CF，BD之间的位置关系为，数量关系为．请利用图2或图3予以证明（选择一个即可）．

（2）如果AB≠AC，∠BAC≠90°，点D在线段BC上运动．且AC=4

2

，BC=3，∠BCA=45°，设正方形ADEF的边DE与线段CF相交于点P，求线段CP长的最大值．