
题目列表(包括答案和解析)
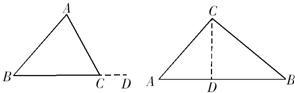
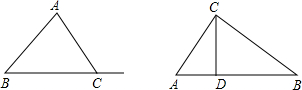
在研究三角形内角和等于180°的证明方法时,小明和小虎分别给出了下列证法.
小明:在△ABC中,延长BC到D,
∴∠ACD=∠A+∠B(三角形一个外角等于和它不相邻的两个内角的和).
又∵∠ACD+∠ACB=180°(平角定义),
∴∠A+∠B+∠ACB=180°(等式的性质).
小虎:在△ABC中,作CD⊥AB(如图),
∵CD⊥AB(已知),
∴∠ADC=∠BDC=90°(直角定义).
∴∠A+∠ACD=90°,∠B+∠BCD=90°(直角三角形两锐角互余).
∴∠A+∠ACD+∠B+∠BCD=180°(等式的性质).
∴∠A+∠B+∠ACB=180°.
请你判断上述两名同学的证法是否正确,如果不正确,写出一种你认为较简单的证明三角形内角和定理的方法,与同伴交流.
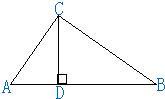 15、如图,∠ACB=90°,CD⊥AB,则图中与∠A互余的角有
15、如图,∠ACB=90°,CD⊥AB,则图中与∠A互余的角有湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com