
题目列表(包括答案和解析)
如图,正方形ABCD的边长为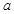 ,点E在AB边上.四边形EFGB也为正方形,设△AFC的面积为S,则 (
)
,点E在AB边上.四边形EFGB也为正方形,设△AFC的面积为S,则 (
)

A.S=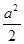 B.S=
B.S=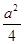
C.S=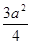 D.S与BE长度有关
D.S与BE长度有关
 如图,正方形ABCD的边长为
如图,正方形ABCD的边长为 ,有一点P在BC上运动,设PB=x,梯形APCD的面积为y.
,有一点P在BC上运动,设PB=x,梯形APCD的面积为y. S梯形APCD,请确定P点的位置.
S梯形APCD,请确定P点的位置. ,点E在AB边上.四边形EFGB也为正方形,设△AFC的面积为S,则 ( )
,点E在AB边上.四边形EFGB也为正方形,设△AFC的面积为S,则 ( )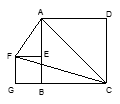
A.S=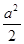 | B.S=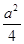 |
C.S=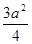 | D.S与BE长度有关 |
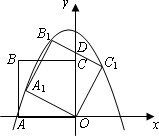
如图,正方形ABCD的边长为![]() ,以O为原点建立平面直角坐标系,点A在x轴的负半轴上,点C在y轴的正半轴上,把正方形ABCO绕点O顺时针旋转α后得到正方形A1B1C1O(α<45°),B1C1交y轴于点D,且D为B1C1的中点,抛物线y=ax2+bx+c过点A1,B1,C1.
,以O为原点建立平面直角坐标系,点A在x轴的负半轴上,点C在y轴的正半轴上,把正方形ABCO绕点O顺时针旋转α后得到正方形A1B1C1O(α<45°),B1C1交y轴于点D,且D为B1C1的中点,抛物线y=ax2+bx+c过点A1,B1,C1.
(1)求tanα的值;
(2)求点A1的坐标,并直接写出点B1、点C1的坐标;
(3)求抛物线的函数表达式及其对称轴;
(4)在抛物线的对称轴上是否存在点P,使△PB1C1为直角三角形,若存在,直接写出所有满足条件的P点坐标;若不存在,请说明理由.
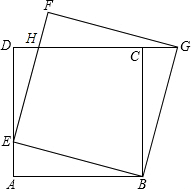 如图,正方形ABCD的边长为1,点E是AD边上的动点,从点A沿AD向D运动,以BE为边,在BE的上方作正方形BEFG,连接CG.请探究:
如图,正方形ABCD的边长为1,点E是AD边上的动点,从点A沿AD向D运动,以BE为边,在BE的上方作正方形BEFG,连接CG.请探究:湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com