
题目列表(包括答案和解析)
甲、乙两公司生产同一种产品,经测算,对于函数g(x)、g(x)及任意的x≥0,当甲公司投入x万元作宣传时,若乙公司投入的宣传费小于f(x)万元,则乙公司有失败的风险,否则无失败风险;当乙公司投入x万元作宣传时,若甲公司投入的宣传费小于g(x)万元,则甲公司有失败的风险,否则无失败风险.
(1)试解释f(0)=11、g(0)=21的实际意义;
(2)当![]() ,
,![]() 时,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用.问此时甲、乙两公司各应投入多少宣传费?
时,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用.问此时甲、乙两公司各应投入多少宣传费?
| x |
甲、乙两公司生产同一种新产品,经测算,对于函数 、
、 及任意的
及任意的 ,当甲公司投入
,当甲公司投入 万元作宣传时,若乙公司投入的宣传费小于
万元作宣传时,若乙公司投入的宣传费小于 万元,则乙公司有失败的风险,否则无失败的风险;当乙公司投入
万元,则乙公司有失败的风险,否则无失败的风险;当乙公司投入 万元作宣传时,若甲公司投入的宣传费小于
万元作宣传时,若甲公司投入的宣传费小于 万元,则甲公司有失败的风险,否则无失败的风险.
万元,则甲公司有失败的风险,否则无失败的风险.
(1)请解释 的实际意义;
的实际意义;
(2)当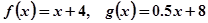 时,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能地少投入宣传费用,问此时甲、乙两公司应各投入多少宣传费用?
时,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能地少投入宣传费用,问此时甲、乙两公司应各投入多少宣传费用?
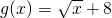 时,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能的少投入宣传费用,问此时甲乙两公司应各投入多少宣传费用?
时,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能的少投入宣传费用,问此时甲乙两公司应各投入多少宣传费用? 时,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司各应投入多少宣传费用?
时,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司各应投入多少宣传费用? 1-12题 AAAAA CDDCD BB
13、等腰梯形;14、 ;15、充分非必要;16、186
;15、充分非必要;16、186
17、
18、解:由 +25+|
+25+| -5
-5 |≥
|≥ ,而
,而 ,等号当且仅当
,等号当且仅当 时成立;且
时成立;且 ,等号当且仅当
,等号当且仅当 时成立;所以,
时成立;所以, ,等号当且仅当
,等号当且仅当 时成立;故
时成立;故 。
。
19、(Ⅰ) 表示当甲公司不投入宣传费时,乙公司要回避失败的风险至少要投入11万元的宣传费;
表示当甲公司不投入宣传费时,乙公司要回避失败的风险至少要投入11万元的宣传费; 表示当乙公司不投入宣传费时,甲公司要回避失败的风险至少要投入21万元的宣传费.
表示当乙公司不投入宣传费时,甲公司要回避失败的风险至少要投入21万元的宣传费.
(Ⅱ)设甲、乙公司投入的宣传费分别为 、
、 万元,当且仅当
万元,当且仅当 ①,
①,
且 ……②时双方均无失败的风险,
……②时双方均无失败的风险,
由①②得 易解得
易解得 ,
,
所以 ,故
,故 .
.
20、解:(1) 令g(x)=f(x)-2x=ln(x+m)-2x, 则g (x)=
(x)= -2
-2
∵x≥2-m ∴x+m≥2 ∴ ≤
≤ 从而g
从而g (x)=
(x)= -2≤
-2≤ -2<0
-2<0
∴g(x)在[2-m, +
 上单调递减 ∴x=2-m时,
上单调递减 ∴x=2-m时,
g(x)=f(x)-2x最大值=ln(2-m+m)-2(2-m)=ln2+
(2) 假设f(x)=x还有另一解x= (
(

 ) 由假设知
) 由假设知
 -
- =f(
=f( )-f(
)-f( )=f
)=f (x
(x )?(
)?( -
- ) x
) x
 [2-m, +
[2-m, +

故f (x
(x )=1, 又∵f
)=1, 又∵f (x
(x )=
)= ≤
≤ <1 矛盾
<1 矛盾
故f(x)=x有唯一解x=
21、
22、解:(1)若
 ,则在定义域内存在
,则在定义域内存在 ,
,
使得 ,∵方程
,∵方程 无解,
无解,
∴
 .
.
 ,
,
当 时,
时, , 当
, 当 时,由
时,由 ,
,
得 。
。
∴ .
.
 ,
,
又∵函数 图象与函数
图象与函数 的图象有交点,设交点的横坐标为
的图象有交点,设交点的横坐标为 ,
,
则 ,其中
,其中 ,
,
∴ ,即
,即 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com