
题目列表(包括答案和解析)
如图,设圆的半径为1,弦心距为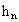 ;正n边形的边长为
;正n边形的边长为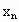 ,面积为
,面积为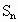 .由勾股定理,得
.由勾股定理,得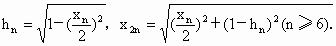
容易知道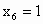 .
.
观察图1,不难发现,正2n边形的面积等于正n边形的面积加上n个等腰三角形的面积,即
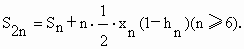
利用这个递推公式,我们可以得到:
正六边形的面积
正十二边形的面积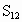 ________;
________;
正二十四边形的面积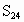 ________;
________;
…
请问n的输入值满足什么条件?n的输出组表示什么?当n不断增大,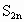 的值不断趋近于什么?用循环结构编写出程序,还用Scilab语言编写一个程序.
的值不断趋近于什么?用循环结构编写出程序,还用Scilab语言编写一个程序.
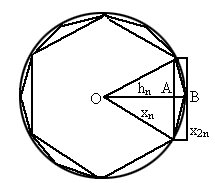
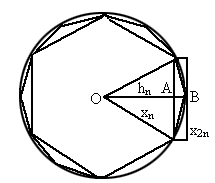
如图,设圆的半径为
1,弦心距为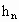 ;正n边形的边长为
;正n边形的边长为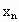 ,面积为
,面积为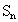 .由勾股定理,得
.由勾股定理,得
容易知道
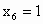 .
.
观察图
1,不难发现,正2n边形的面积等于正n边形的面积加上n个等腰三角形的面积,即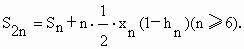
利用这个递推公式,我们可以得到:
正六边形的面积
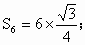
正十二边形的面积
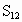 ________;
________;
正二十四边形的面积
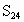 ________;
________;
…
请问
n的输入值满足什么条件?n的输出组表示什么?当n不断增大,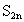 的值不断趋近于什么?用循环结构编写出程序,还用Scilab语言编写一个程序.
的值不断趋近于什么?用循环结构编写出程序,还用Scilab语言编写一个程序.
已知 中,内角
中,内角 的对边的边长分别为
的对边的边长分别为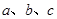 ,且
,且
(I)求角 的大小;
的大小;
(II)若 求
求 的最小值.
的最小值.
【解析】第一问,由正弦定理可得:sinBcosC=2sinAcosB-sinCcosB,即sin(B+C)=2sinAcosB,
第二问,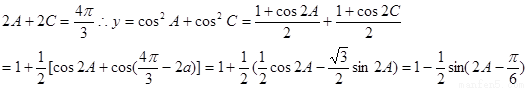
三角函数的性质运用。
解:(Ⅰ)由正弦定理可得:sinBcosC=2sinAcosB-sinCcosB,即sin(B+C)=2sinAcosB,
(Ⅱ)由(Ⅰ)可知
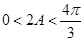 ,
, ,则当
,则当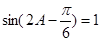 ,即
,即 时,y的最小值为
时,y的最小值为 .
.
已知函数 .]
.]
(1)求函数 的最小值和最小正周期;
的最小值和最小正周期;
(2)设 的内角
的内角 、
、 、
、 的对边分别为
的对边分别为 ,
, ,
, ,且
,且 ,
, ,
,
若 ,求
,求 ,
, 的值.
的值.
【解析】第一问利用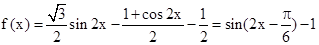
得打周期和最值
第二问

 ,由正弦定理,得
,由正弦定理,得 ,①
,①
由余弦定理,得 ,即
,即 ,②
,②
由①②解得
设△ABC的内角A、B、C所对的边分别为a、b、c,已知a=1,b=2,cosC=. (1)求△ABC的周长; (2)求cos(A-C)的值.
【解析】(1)借助余弦定理求出边c,直接求周长即可.(2)根据两角差的余弦公式需要求sinC,sinA,cosA,由正弦定理即可求出sinA,进而可求出cosA.sinC可由cosA求出,问题得解.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com