
题目列表(包括答案和解析)
 A.(选修4-4坐标系与参数方程)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线ρsin(θ+
A.(选修4-4坐标系与参数方程)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线ρsin(θ+| π | 3 |
 A.(不等式选做题)若关于x的不等式|x+3|-|x+2|≥log2a有解,则实数a的取值范围是:
A.(不等式选做题)若关于x的不等式|x+3|-|x+2|≥log2a有解,则实数a的取值范围是:| PB |
| PA |
| 1 |
| 2 |
| PC |
| PD |
| 1 |
| 3 |
| BC |
| AD |
|
| 2 |
| cosθ-sinθ |
| 2 |
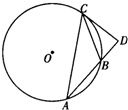 A.(不等式选做题)
A.(不等式选做题)| 3 |
| π |
| 3 |
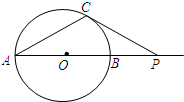 A.不等式
A.不等式| x-2 |
| x2+3x+2 |
| 3 |
|
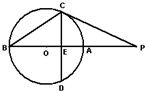 A.(不等式选做题)不等式|3x-6|-|x-4|>2x的解集为
A.(不等式选做题)不等式|3x-6|-|x-4|>2x的解集为| π |
| 4 |
| 2 |
一、选择题:本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,选择一个符合题目要求的选项.
(1)C (2)B (3)D (4)C (5)B (6)B
(7)A (8)C (9)B (10)D (11)A (12)B
二、填空题:本大题共4小题,每小题4分,共16分. 答案填在题中横线上.
13. 如果一个二面角的两个面与另一个二面角的两个面分别垂直,则这两个二面角相等或互补 假 14. 15. 0 16.
15. 0 16.
三、解答题:本大题共6小题,共74分. 解答应写出文字说明、证明过程或演算步骤.
17. 解:(Ⅰ) ………2分
………2分
 ………4分
………4分
 ………6分
………6分
(II)
 ……8分
……8分
 的图象与x轴正半轴的第一个交点为
的图象与x轴正半轴的第一个交点为 ………10分
………10分
所以 的图象、y轴的正半轴及x轴的正半轴三者围成图形的面积
的图象、y轴的正半轴及x轴的正半轴三者围成图形的面积
 =
= …12分
…12分
18. 解:(Ⅰ)设摇奖一次,获得一、二、三、四、五等奖的事件分别记为 .
.
则其概率分别为



 ……3分
……3分
设摇奖一次支出的学习用品相应的款项为 ,则的分布列为:
,则的分布列为:

1
2
3
4
5






 .………6分
.………6分
若捐款10元者达到1500人次,那么购买学习用品的款项为 (元),
(元),
除去购买学习用品的款项后,剩余款项为 (元),
(元),
故剩余款项可以帮助该生完成手术治疗. ………8分
(II)记事件“学生甲捐款20元获得价值6元的学习用品”为 ,则
,则 .
.
即学生甲捐款20元获得价值6元的学习用品的概率为 ………12分
………12分
19. 以D为原点,以DA、DC、DD1所在直线分别为x轴,z轴建立空间直角坐标系D―xyz如图,则有A(2,0,0),B(2,2,0),C(0,2,0),A1(1,0,2),B1(1,1,2),C1(0,1,2),D1(0,0,2). … 3分
(Ⅰ)证明:设 则有
则有 所以
所以 ,
,
 ,∴
,∴ 平面
平面 ;………6分
;………6分
 (II)解:
(II)解:
设 为平面
为平面 的法向量,
的法向量,

于是
 ………8分
………8分
同理可以求得平面 的一个法向量
的一个法向量 ,………10分
,………10分
 ∴二面角
∴二面角 的余弦值为
的余弦值为 . ………12分
. ………12分
20. 解:(Ⅰ)对 求导数,得
求导数,得 ,切点是
,切点是 的切线方程是
的切线方程是 .…2分
.…2分
当 时,切线过点
时,切线过点 ,即
,即 ,得
,得 ;
;
当 时,切线过点
时,切线过点 ,即
,即 ,得
,得 .
.
所以数列 是首项
是首项 ,公比为
,公比为 的等比数列,
的等比数列,
所以数列 的通项公式为
的通项公式为 .………4分
.………4分
(II)当 时,
时, 数列
数列 的前
的前 项和
项和 =
=
同乘以 ,得
,得 =
= 两式相减,…………8分
两式相减,…………8分
得 =
= ,
,
所以 =
= .………12分
.………12分
21.解:(Ⅰ)由于 所以
所以
 ………2分
………2分
令 ,
,
当a=2时,
所以2-a≠0.
①
当2-a>0,即a<2时, 的变化情况如下表1:
的变化情况如下表1:
x

0
(0,2-a)
2-a
(2-a,+∞)

-
0
+
0
-

ㄋ
极小值
ㄊ
极大值
ㄋ
此时应有f(0)=0,所以a=0<2;
②当2-a<0,即a>2时, 的变化情况如下表2:
的变化情况如下表2:
x

2-a
(2-a,0)
0
(0,+∞)

-
0
+
0
-

ㄋ
极小值
ㄊ
极大值
ㄋ
此时应有
而
综上可知,当a=0或4时, 的极小值为0. ………6分
的极小值为0. ………6分
(II)若a<2,则由表1可知,应有 也就是
也就是

设
由于a<2得 
所以方程  无解. ………8分
无解. ………8分
若a>2,则由表2可知,应有f(0)=3,即a=3. ………10分
综上可知,当且仅当a=3时,f(x)的极大值为3. ………12分
22. 解:(Ⅰ)由 得,
得, ;……4分
;……4分
由直线 与圆
与圆 相切,得
相切,得 ,所以,
,所以, 。所以椭圆的方程是
。所以椭圆的方程是 .……4分
.……4分
(II)由条件知, ,即动点
,即动点 到定点
到定点 的距离等于它到直线
的距离等于它到直线 :
: 的距离,由抛物线的定义得点
的距离,由抛物线的定义得点 的轨迹
的轨迹 的方程是
的方程是 . ……8分
. ……8分
(III)由(2)知 ,设
,设 ,
, ,所以
,所以
 ,
, .
.
由 ,得
,得 .因为
.因为 ,化简得
,化简得 ,……10分
,……10分
 (当且仅当
(当且仅当 ,即
,即 时等号成立). ……12分
时等号成立). ……12分  ,又
,又
所以当 ,即
,即 时,
时, ,故
,故 的取值范围是
的取值范围是 .14分
.14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com