
题目列表(包括答案和解析)
 如图,BD、CD分别是∠ABC和∠ACB的角平分线,BD、CD相交于点D,试探索∠A与∠D之间的数量关系,并证明你的结论.
如图,BD、CD分别是∠ABC和∠ACB的角平分线,BD、CD相交于点D,试探索∠A与∠D之间的数量关系,并证明你的结论. 如图,BD、CD分别是∠ABC和∠ACB的角平分线,BD、CD相交于点D,试探索∠A与∠D之间的数量关系,并证明你的结论.
如图,BD、CD分别是∠ABC和∠ACB的角平分线,BD、CD相交于点D,试探索∠A与∠D之间的数量关系,并证明你的结论.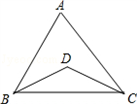
| M(l) |
| M(l) |
| M(m) |
| M(m) |
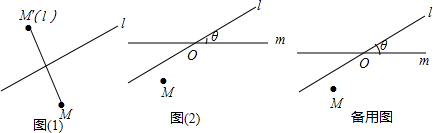
 ,点M的轴对称点就记为M′(l),如图(1)所示.如果先作平面上的点M关于直线l的轴对称变换
,点M的轴对称点就记为M′(l),如图(1)所示.如果先作平面上的点M关于直线l的轴对称变换 ,得到对应点M′(l),然后,再作M′(l)关于另外一条直线m的轴对称变换
,得到对应点M′(l),然后,再作M′(l)关于另外一条直线m的轴对称变换 ,这样点M就与该点关于直线l和m的轴对称点M′′(l,m)之间建立了一种对应关系,我们把这种对应关系就叫做点M关于直线l和m的轴对称变换,记为
,这样点M就与该点关于直线l和m的轴对称点M′′(l,m)之间建立了一种对应关系,我们把这种对应关系就叫做点M关于直线l和m的轴对称变换,记为 ,M的对应点就记为M′′(l,m).如图(2),M是平面上的一点,直线l、m相交所成的角为θ(0°<θ≤90°),且交点为O,请回答如下问题:
,M的对应点就记为M′′(l,m).如图(2),M是平面上的一点,直线l、m相交所成的角为θ(0°<θ≤90°),且交点为O,请回答如下问题: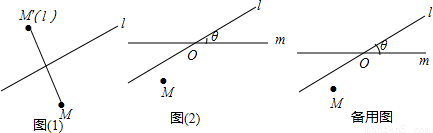
一、选择题(每小题3分,共24分)
1
2
3
4
5
6
7
8
C
C
B
D
C
A
C
A
二、填空题(每小题3分,共30分)
9. 10.45
11.(0,2) 12.①,②,④
10.45
11.(0,2) 12.①,②,④
13. 14.45
15.
14.45
15.  16.65
16.65
17. 18.-2≤a≤2
18.-2≤a≤2
三、(每小题8分,共32分)
19.(1)解:原式= ……………………………………………………2分
……………………………………………………2分
= ……………………………………………………………3分
……………………………………………………………3分
=2.…………………………………………………………………4分
(2)解:原式= …………………………2分
…………………………2分
 ………………………………………………………3分
………………………………………………………3分
 .………………………………………………………………4分
.………………………………………………………………4分
20.解: (1)△ACE≌△A
 (2)∵△ABC≌△A1B
(2)∵△ABC≌△A1B
∴AC= A
∴A C1=A
已知∠A=∠A1 ,∠ACE=∠A
∴△ACE≌△A
∴CE=C1 E1,…………………………………………………………………………7分
又∵BC= B
∴B1E1= BE.…………………………………………………………………………8分
21.解:(1)P(抽到偶数)= ;…………………………………………………3分
;…………………………………………………3分
(2)所有可能两位数列举如下:12,13,21,23,31,32.…………………6分
这个两位数是奇数的概率是 .………………………………………………………8分
.………………………………………………………8分
22.(1)解:  .…………4分
.…………4分
答:这三家大医院3月份出生的总人数中男宝宝的百分比为53%. ……………5分
(2) (人).………………………………………………8分
(人).………………………………………………8分
答:估计3月份南京共有2650名男宝宝出生.
 |
四、(每题10分,共40分)
23.解:(1)画图. ………………………………4分
(2)画图. ……………………………………5分
AC=4, ………………………………7分
C旋转到C1所经过的路线长等于2π. ……10分
24.解:(1)把A(1,3)代入y=,得k=3, …………………………2分
 把B(n,-1)代入y=,得n=-3,
把B(n,-1)代入y=,得n=-3,
所以B(-3,-1).………………………………4分
把A(1,3),B(-3,-1)代入y=mx+b,
解得,m=1,b=2. ………………………………6分
所以,反比例函数的关系式是y= ,
一次函数的函数关系式是y=x+2. …………………………………………8分
(2)点P的坐标可以是(-3,-1)或(3,1)或其它.………………10分
 25.解:(1)如图,在
25.解:(1)如图,在 中,
中,
 (m).……2分
(m).……2分
在 中,
中,
 (m),……………4分
(m),……………4分
 m. ………………………………5分
m. ………………………………5分
即改善后的台阶坡面会加长 m.
m.
(2)如图,在 中,
中, (m).………6分
(m).………6分
在 中,
中,
 (m),……………………………8分
(m),……………………………8分
 (m).………………………9分
(m).………………………9分
即改善后的台阶多占 .长的一段水平地面. ……………………10分
.长的一段水平地面. ……………………10分
26.(1)当射线BA绕点B按顺时针方向旋转60度或120度时与⊙O相切.…1分
 理由:当BA绕点B按顺时针方向旋转60度到B A′的位置.
理由:当BA绕点B按顺时针方向旋转60度到B A′的位置.
则∠A′BO=30°,
过O作OG⊥B A′垂足为G,
∴OG= OB=2. …………………………3分
OB=2. …………………………3分
∴B A′是⊙O的切线.……………………4分
同理,当BA绕点B按顺时针方向旋转120度到B A″的位置时,
B A″也是⊙O的切线.…………………6分
(如只有一个答案,且说理正确,给2分)
(或:当BA绕点B按顺时针方向旋转到B A′的位置时,BA与⊙O相切,
设切点为G,连结OG,则OG⊥AB,
∵OG= OB,∴∠A′BO=30°.
OB,∴∠A′BO=30°.
∴BA绕点B按顺时针方向旋转了60度.
同理可知,当BA绕点B按顺时针方向旋转到B A″的位置时,BA与⊙O相切,BA绕点B按顺时针方向旋转了120度.)
(2)∵MN= ,
, OM=ON=2,
OM=ON=2,
∴MN 2 =
∴∠MON=90°. …………………8分
∴的长为 =π.…………10分
=π.…………10分
五、(每题12分,共24分)
27.解:(1)①  .………………………………………………2分
.………………………………………………2分
②  ………6分
………6分
= .………………………………………7分
.………………………………………7分
当x=1时,y有最大值,且最大值为 .………………………8分
.………………………8分
(2)画法:以B为圆心,BD长为半径画弧,交AB于点E,则点E即为所求…10分
画图正确 …………………………………………………………………12分
28.解:(1)每画对一个给2分.………………………………………………4分
(2)D.……………………………………………………………………………7分
(3)① 判断: .……………………………………8分
.……………………………………8分
证明:如图(1),由轴对称性质可知, 垂直平分
垂直平分 ,
,
则 为等腰三角形.………………………………………………10分
为等腰三角形.………………………………………………10分
∵ .同理
.同理 ,………………………………………………11分
,………………………………………………11分
∴ .…………………………………………………12分
.…………………………………………………12分
②判断: .
.
证明:如图(2),连接 、
、 、
、 .
.
∵M, 关于直线
关于直线 成轴对称,
成轴对称,
∴ 是
是 的垂直平分线.
的垂直平分线.
∴ .………………………………………………………………10分
.………………………………………………………………10分
同理可得: .……………………………………………11分
.……………………………………………11分
∴ .…………………………………………………………12分
.…………………………………………………………12分
 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com