
题目列表(包括答案和解析)
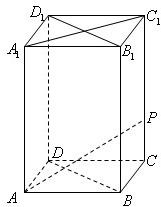 如图,在底面边长为1,侧棱长为2的正四棱柱ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m.
如图,在底面边长为1,侧棱长为2的正四棱柱ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m.(10分)如图,在底面边长为1,侧棱长为2的正四棱柱![]() 中,P是侧棱
中,P是侧棱![]() 上的一点,
上的一点,![]() .
.
(1)试确定m,使直线AP与平面BDD1B1所成角为60º;
(2)在线段![]() 上是否存在一个定点
上是否存在一个定点![]() ,使得对任意的m,
,使得对任意的m,![]() ⊥AP,并证明你的结论.
⊥AP,并证明你的结论.

如图,在底面边长为1,侧棱长为2的正四棱柱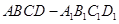 中,P是侧棱
中,P是侧棱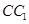 上的一点,
上的一点,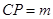 .
.
(1)试确定m,使直线AP与平面BDD1B1所成角为60º;
(2)在线段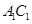 上是否存在一个定点
上是否存在一个定点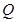 ,使得对任意的m,
,使得对任意的m,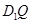 ⊥AP,并证明你的结论.
⊥AP,并证明你的结论. 

如图,在底面边长为1,侧棱长为2的正四棱柱![]() 中,P是侧棱
中,P是侧棱![]() 上的一点,
上的一点,![]() . (1)试确定m,使直线AP与平面BDD1B1所成角为60º;(2)在线段
. (1)试确定m,使直线AP与平面BDD1B1所成角为60º;(2)在线段![]() 上是否存在一个定点
上是否存在一个定点![]() ,使得对任意的m,
,使得对任意的m,![]() ⊥AP,并证明你的结论.
⊥AP,并证明你的结论.

必做题部分
一、填空题:本大题共14小题,每小题5分,共70分.
1. 已知全集U={1,2,3,4,5},集合A={1,3,5},则 ▲ .
▲ .
 2. 若复数z满足zi=2+i(i是虚数单位),则z= ▲ .
2. 若复数z满足zi=2+i(i是虚数单位),则z= ▲ .
3. 已知幂函数 的图象过点
的图象过点 ,则
,则
 = ▲ .
= ▲ .
4. 如图,一个空间几何体的主视图、左视图、俯视图为全
等的等腰直角三角形,如果直角三角形的直角边长为1,
那么这个几何体的表面积为 ▲ .
5. 设x0是方程8-x=lgx的解,且 ,则k= ▲ .
,则k= ▲ .
6. 矩形ABCD中, . 在矩形内任取一点P,则
. 在矩形内任取一点P,则 的概率为 ▲
.
的概率为 ▲
.
7. △ABC中, ,
, ,则
,则 的最小值是 ▲
.
的最小值是 ▲
.
 8. 已知
8. 已知 ,
, ,则
,则 等于 ▲
.
等于 ▲
.
9. 右图是由所输入的x值计算y值的一个算法程序,
若x依次取数列 (
( ,n≤2009)的
,n≤2009)的
项,则所得y值中的最小值为 ▲ .
11. 已知双曲线
 的左、右焦点分别为F1、F2,P是双曲线上一点,且PF1⊥PF2,P F1
的左、右焦点分别为F1、F2,P是双曲线上一点,且PF1⊥PF2,P F1 P F2 =4ab,则双曲线的离心率是 ▲
.
P F2 =4ab,则双曲线的离心率是 ▲
.
11. 设函数f(x)=ax+b,其中a,b为常数,f1(x)=f(x),fn+1(x)=f [fn(x)],n=1,2,….
若f5(x)=32x+93, 则ab= ▲ .
12.
函数f(x)= 的值域为 ▲
.
的值域为 ▲
.
13. 设函数 , A0为坐标原点,An为函数y=f(x)图象上横坐标为
, A0为坐标原点,An为函数y=f(x)图象上横坐标为
的点,向量 ,向量i=(1,0),设
,向量i=(1,0),设 为向量
为向量 与向量i的夹角,则满足
与向量i的夹角,则满足
 的最大整数n是 ▲
.
的最大整数n是 ▲
.
14. 已知l1和l2是平面内互相垂直的两条直线,它们的交点为A,动点B、C分别在l1和l2
上,且 ,过A、B、C三点的动圆所形成的区域的面积为 ▲
.
,过A、B、C三点的动圆所形成的区域的面积为 ▲
.
【填空题答案】
1.{2,4}; 2.1-2i ;
3. ;
4.
;
4. ; 5.7;
; 5.7;
6. ; 7.
; 7. ; 8.
; 8. ; 9.17; 10.
; 9.17; 10. ;
;
11.6; 12. ;
13.3;
14.18
;
13.3;
14.18 .
.
二、解答题:本大题共6小题,共90分,解答应写出文字说明,证明过程或演算步骤.
15. (本题满分14分)
某高级中学共有学生3000名,各年级男、女生人数如下表:
高一年级
高二年级
高三年级
女生
523
x
y
男生
487
490
z
已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0.17.
(1)问高二年级有多少名女生?
(2)现对各年级用分层抽样的方法在全校抽取300名学生,问应在高三年级抽取多少
名学生?
【解】(1)由题设可知 , 所以x=510. ………………………6分
, 所以x=510. ………………………6分
(2)高三年级人数为y+z=3000-(523+487+490+510)=990,………………9分
现用分层抽样的方法在全校抽取300名学生,应在高三年级抽取的人数为:
 名. ………………………12分
名. ………………………12分
答:(1)高二年级有510名女生;(2)在高三年级抽取99名学生.……………14分
 16. (本题满分14分)
16. (本题满分14分)
如图, ABCD为矩形,CF⊥平面ABCD,DE⊥平面ABCD,
AB=
(1)求证:平面PCF⊥平面PDE;
(2)求四面体PCEF的体积.
【证明】(1)因为ABCD为矩形,AB=2BC, P为AB的中点,
所以三角形PBC为等腰直角三角形,∠BPC=45°. …………………………2分
同理可证∠APD=45°.
所以∠DPC=90°,即PC⊥PD. …………………………3分
又DE⊥平面ABCD,PC在平面ABCD内,所以PC⊥DE. ………………………4分
因为DE∩PD=D ,所以PC ⊥PDE . …………………………5分
又因为PC在平面PCF内,所以平面PCF⊥平面PDE. …………………………7分
【解】(2)因为CF⊥平面ABCD,DE⊥平面ABCD,
所以DE//CF. 又DC⊥CF,
所以 ……………………… 10分
……………………… 10分
在平面ABCD内,过P作PQ⊥CD于Q,则
PQ//BC,PQ=BC=
因为BC⊥CD,BC⊥CF,
所以BC⊥平面PCEF,即PQ⊥平面PCEF,
亦即P到平面PCEF的距离为PQ=
 ………………………14分
………………………14分
(注:本题亦可利用 求得)
求得)
17 . (本题满分15分)
△ABC中,角A的对边长等于2,向量m= ,向量n=
,向量n= .
.
(1)求m?n取得最大值时的角A的大小;
(2)在(1)的条件下,求△ABC面积的最大值.
【解】(1)m?n=2 -
- . …………………3分
. …………………3分
因为
A+B+C ,所以B+C
,所以B+C -A,
-A,
于是m?n= +cosA=-2
+cosA=-2 =-2
=-2 .……………5分
.……………5分
因为 ,所以当且仅当
,所以当且仅当 =
= ,即A=
,即A= 时,m?n取得最大值
时,m?n取得最大值 .
.
故m?n取得最大值时的角A= .
…………………………7分
.
…………………………7分
(2)设角A、B、C所对的边长分别为a、b、c,
由余弦定理,得 b2+c2-a2=2bccosA, …………………………9分
即bc+4=b2+c2≥2bc, ……………………… 11分
所以bc≤4,当且仅当b=c=2时取等号. ……………………… 12分
又S△ABC= bcsinA=
bcsinA= bc≤
bc≤ .
.
当且仅当a=b=c=2时,△ABC的面积最大为 . ………………………15分
. ………………………15分
18. (本题满分15分)
在平面直角坐标系xOy中,矩形OABC的边OA、OC分别在x轴和y轴上(如图),且
OC=1,OA=a+1(a>1),点D在边OA上,满足OD=a. 分别以OD、OC为长、短半轴的
椭圆在 矩形及其内部的部分为椭圆弧CD. 直线l:y=-x+b与椭圆弧相切,与AB交于
矩形及其内部的部分为椭圆弧CD. 直线l:y=-x+b与椭圆弧相切,与AB交于
点E.
(1)求证: ;
;
(2)设直线l将矩形OABC分成面积相等的两部分,
求直线l的方程;
(3)在(2)的条件下,设圆M在矩形及其内部,
且与l和线段EA都相切,求面积最大的圆M
的方程.
【解】题设椭圆的方程为 .
…………………………1分
.
…………………………1分
由 消去y得
消去y得 . …………………………2分
. …………………………2分
由于直线l与椭圆相切,故△=(-
化简得 .
①
…………………………4分
.
①
…………………………4分
(2)由题意知A(a+1,0),B(a+1,1),C(0,1),
于是OB的中点为 .
…………………………5分
.
…………………………5分
因为l将矩形OABC分成面积相等的两部分,所以l过点 ,
,
即 ,亦即
,亦即 .
②
…………………………6分
.
②
…………………………6分
由①②解得 ,故直线l的方程为
,故直线l的方程为 …………………………8分
…………………………8分
(3)由(2)知 .
.
因为圆M与线段EA相切,所以可设其方程为 .………9分
.………9分
因为圆M在矩形及其内部,所以 ④ ……………………… 10分
④ ……………………… 10分
圆M与 l相切,且圆M在l上方,所以 ,即
,即 .
.
………………………12分
代入④得 即
即 ………………………13分
………………………13分
所以圆M面积最大时, ,这时,
,这时, .
.
故圆M面积最大时的方程为 ………………………15分
………………………15分
19. (本题满分16分)
已知函数 的导数为
的导数为 . 记函数
. 记函数

 k为常数).
k为常数).
(1)若函数f(x)在区间 上为减函数,求
上为减函数,求 的取值范围;
的取值范围;
(2)求函数f(x)的值域.
【解】(1)因为f(x)在区间 上为减函数,
上为减函数,
所以对任意的 且
且 恒有
恒有 成立.
成立.
即 恒成立. …………………………3分
恒成立. …………………………3分
因为 ,所以
,所以 对
对 且
且 时,恒成立.
时,恒成立.
又 <1,所以
<1,所以 …………………………6分
…………………………6分
(2) .
…………………………7分
.
…………………………7分
下面分两种情况讨论:
(1)当 时,
时, 是关于x的增函数,值域为
是关于x的增函数,值域为
…………………………9分
(2)当 时,又分三种情况:
时,又分三种情况:
①当 时,因为
时,因为 ,所以
,所以 即
即 .
.
所以f(x)是减函数, .
.
又 ,
,
当 ,所以f(x)值域为
,所以f(x)值域为 .
………………………10分
.
………………………10分
②当k=1时, ,
,
且f(x)是减函数,故f(x)值域是 .
………………………12分
.
………………………12分
③当 时,
时, 是增函数,
是增函数, ,
,
 .
.
下面再分两种情况:
(a)当 时,
时, 的唯一实根
的唯一实根 ,故
,故 ,
,
 是关于x的增函数,值域为
是关于x的增函数,值域为 ;
;
(b)当 时,
时, 的唯一实根
的唯一实根 ,
,
当 时,
时, ;当
;当 时,
时, ;
;
所以f(x) .
.
故f(x)的值域为 .
………………………15分
.
………………………15分
综上所述,f(x)的值域为 ;
; (
( );
);
 (
( );
); (
( ). ………………………16分
). ………………………16分
20.(本题满分16分)
设{an}是等差数列,其前n项的和为Sn.
(1)求证:数列 为等差数列;
为等差数列;
(2)设{an}各项为正数,a1= ,a1≠a2,若存在互异正整数m,n,p满足:①m+p=2n;
,a1≠a2,若存在互异正整数m,n,p满足:①m+p=2n;
② . 求集合
. 求集合 的元素个数;
的元素个数;
(3)设bn= (a为常数,a>0,a≠1,a1≠a2),数列{bn}前n项和为Tn. 对于正整数c,
(a为常数,a>0,a≠1,a1≠a2),数列{bn}前n项和为Tn. 对于正整数c,
d,e,f,若c<d<e<f,且c+f=d+e, 试比较(Tc)-1+(Tf)-1与(Td)-1+(Te)-1的大小.
【证】(1){an}为等差数列,设其公差为 ,则
,则
 ,于是
,于是 (常数),
(常数),
故数列 是等差数列.
…………………………3分
是等差数列.
…………………………3分
【解】(2)因为{an}为等差数列,所以 是等差数列,
是等差数列,
于是可设 为常数),从而
为常数),从而 .
.
因为m+p=2n,所以由 两边平方得
两边平方得
 ,即
,即 ,
,
亦即 ,………………………4分
,………………………4分
于是 ,两边平方并整理得
,两边平方并整理得 ,即
,即 .
.
…………………………6分
因为m≠p,所以 ,从而
,从而 ,而a1=
,而a1= ,所以
,所以 .
.
故
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com