
题目列表(包括答案和解析)
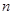 (
( )个大小相同的球,其中有3个红球和
)个大小相同的球,其中有3个红球和 个白球.已知从口袋中随机取出一个球是红球的概率是
个白球.已知从口袋中随机取出一个球是红球的概率是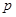 .
. 时,不放回地从口袋中随机取出3个球,求取到白球的个数
时,不放回地从口袋中随机取出3个球,求取到白球的个数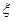 的期望
的期望 ;
; ,有放回地从口袋中连续地取四次球(每次只取一个球),在四次摸球中恰好取到两次红球的概率大于
,有放回地从口袋中连续地取四次球(每次只取一个球),在四次摸球中恰好取到两次红球的概率大于 ,求
,求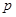 和
和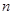 .
.一盒子中有8个大小完全相同的小球,其中3个红球,2个白球,3个黑球.(Ⅰ)若不放回地从盒中连续取两次球,每次取一个,求在第一次取到红球的条件下,第二次也取到红球的概率;(Ⅱ)若从盒中任取3个球,求取出的3个球中红球个数X的分布列和数学期望.

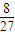
(本小题满分12分)
一个口袋内有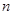 (
(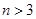 )个大小相同的球,其中有3个红球和
)个大小相同的球,其中有3个红球和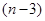 个白球.已知从口袋中随机取出一个球是红球的概率是
个白球.已知从口袋中随机取出一个球是红球的概率是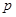 .
.
(1)当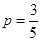 时,不放回地从口袋中随机取出3个球,求取到白球的个数
时,不放回地从口袋中随机取出3个球,求取到白球的个数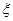 的期望
的期望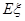 ;
;
(2)若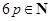 ,有放回地从口袋中连续地取四次球(每次只取一个球),在四次摸球中恰好取到两次红球的概率大于
,有放回地从口袋中连续地取四次球(每次只取一个球),在四次摸球中恰好取到两次红球的概率大于 ,求
,求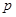 和
和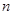 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com