
题目列表(包括答案和解析)
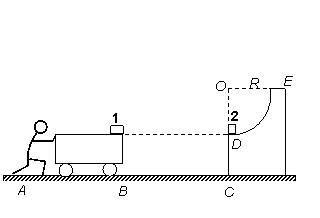
如图所示,一辆质量为M的小车静止在水平面上,车面上右端点有一可视为质点的滑块1,水平面上有与车右端相距为4R的固定的1/4光滑圆弧轨道,其圆周半径为R,圆周E处的切线是竖直的,车上表面与地面平行且与圆弧轨道的末端D等高,在圆弧轨道的最低点D处,有另一个可视为质点的滑块2,两滑块质量均为m。某人由静止开始推车,当车与圆弧轨道的竖直壁CD碰撞后人即撤去推力并离开小车,车碰后靠着竖直壁静止但不粘连,滑块1和滑块2则发生碰撞,碰后两滑块牢牢粘在一起不再分离。车与地面的摩擦不计,滑块1、2与车面的摩擦系数均为![]() ,重力加速度为
,重力加速度为![]() ,滑块与车面的最大静摩擦力可认为等于滑动摩擦力。
,滑块与车面的最大静摩擦力可认为等于滑动摩擦力。
(1)若人推车的力是水平方向且大小为![]() ,则在人推车的过程中,滑块1与车是否会发生相对运动?
,则在人推车的过程中,滑块1与车是否会发生相对运动?
(2)在(1)的条件下,滑块1与滑块2碰前瞬间,滑块1的速度多大?
(3)若车面的长度为![]() ,小车质量
,小车质量![]() ,则
,则![]() 的取值在什么范围内,两个滑块最终没有滑离车面?
的取值在什么范围内,两个滑块最终没有滑离车面?
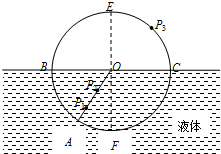
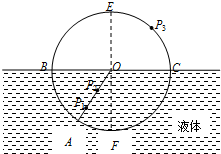 一个物理兴趣小组的同学根据所学光学知识,设计了一个直接测液体折射率的装置.如图是这个装置的示意图,其中的圆是一个圆盘,两条直线BC、EF是在圆盘上所画的两条相互垂直的直径,它们分别代表界面和法线.P1、P2是插在圆盘上的两枚大头针,大头针与圆盘表面垂直且在圆盘的同一半径上.每次测量时让圆盘的下半部分竖直浸入液体中,并保持圆盘上的直线BC与液面相平,然后在圆盘右上方区域观察大头针P1、P2,用一枚大头针P3沿圆周EC部分移动,使其挡住P1、P2,这样只要根据此时P3的位置,就可以直接读出待测液体折射率的值.若测得∠AOF=30°,OP3与OC之间的夹角为45°,则在此时P3所在位置标注的折射率值应为
一个物理兴趣小组的同学根据所学光学知识,设计了一个直接测液体折射率的装置.如图是这个装置的示意图,其中的圆是一个圆盘,两条直线BC、EF是在圆盘上所画的两条相互垂直的直径,它们分别代表界面和法线.P1、P2是插在圆盘上的两枚大头针,大头针与圆盘表面垂直且在圆盘的同一半径上.每次测量时让圆盘的下半部分竖直浸入液体中,并保持圆盘上的直线BC与液面相平,然后在圆盘右上方区域观察大头针P1、P2,用一枚大头针P3沿圆周EC部分移动,使其挡住P1、P2,这样只要根据此时P3的位置,就可以直接读出待测液体折射率的值.若测得∠AOF=30°,OP3与OC之间的夹角为45°,则在此时P3所在位置标注的折射率值应为| 2 |
| 2 |
 光滑圆弧轨道,其圆周半径为R,圆周E处的切线是竖直的,车上表面与地面平行且与圆弧轨道的末端D等高,在圆弧轨道的最低点D处,有另一个可视为质点的滑块2,两滑块质量均为m.某人由静止开始推车,当车与圆弧轨道的竖直壁CD碰撞后人即撤去推力并离开小车,车碰后靠着竖直壁静止但不粘连,滑块1和滑块2则发生碰撞,碰后两滑块牢牢粘在一起不再分离.车与地面的摩擦不计,滑块1、2与车面的摩擦系数均为μ,重力加速度为g,滑块与车面的最大静摩擦力可认为等于滑动摩擦力.
光滑圆弧轨道,其圆周半径为R,圆周E处的切线是竖直的,车上表面与地面平行且与圆弧轨道的末端D等高,在圆弧轨道的最低点D处,有另一个可视为质点的滑块2,两滑块质量均为m.某人由静止开始推车,当车与圆弧轨道的竖直壁CD碰撞后人即撤去推力并离开小车,车碰后靠着竖直壁静止但不粘连,滑块1和滑块2则发生碰撞,碰后两滑块牢牢粘在一起不再分离.车与地面的摩擦不计,滑块1、2与车面的摩擦系数均为μ,重力加速度为g,滑块与车面的最大静摩擦力可认为等于滑动摩擦力.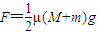 ,则在人推车的过程中,滑块1与车是否会发生相对运动?
,则在人推车的过程中,滑块1与车是否会发生相对运动?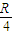 ,小车质量M=km,则k的取值在什么范围内,两个滑块最终没有滑离车面?
,小车质量M=km,则k的取值在什么范围内,两个滑块最终没有滑离车面?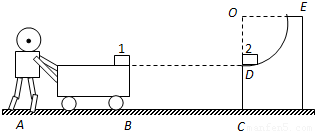
 光滑圆弧轨道,其圆周半径为R,圆周E处的切线是竖直的,车上表面与地面平行且与圆弧轨道的末端D等高,在圆弧轨道的最低点D处,有另一个可视为质点的滑块2,两滑块质量均为m.某人由静止开始推车,当车与圆弧轨道的竖直壁CD碰撞后人即撤去推力并离开小车,车碰后靠着竖直壁静止但不粘连,滑块1和滑块2则发生碰撞,碰后两滑块牢牢粘在一起不再分离.车与地面的摩擦不计,滑块1、2与车面的摩擦系数均为μ,重力加速度为g,滑块与车面的最大静摩擦力可认为等于滑动摩擦力.
光滑圆弧轨道,其圆周半径为R,圆周E处的切线是竖直的,车上表面与地面平行且与圆弧轨道的末端D等高,在圆弧轨道的最低点D处,有另一个可视为质点的滑块2,两滑块质量均为m.某人由静止开始推车,当车与圆弧轨道的竖直壁CD碰撞后人即撤去推力并离开小车,车碰后靠着竖直壁静止但不粘连,滑块1和滑块2则发生碰撞,碰后两滑块牢牢粘在一起不再分离.车与地面的摩擦不计,滑块1、2与车面的摩擦系数均为μ,重力加速度为g,滑块与车面的最大静摩擦力可认为等于滑动摩擦力.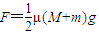 ,则在人推车的过程中,滑块1与车是否会发生相对运动?
,则在人推车的过程中,滑块1与车是否会发生相对运动?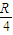 ,小车质量M=km,则k的取值在什么范围内,两个滑块最终没有滑离车面?
,小车质量M=km,则k的取值在什么范围内,两个滑块最终没有滑离车面?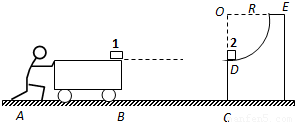
一、选择题(本大题共12小题,每小题5分,共60分)
1~5 D A B D C 6~
二、填空题(本大题共4小题,每小题4分,共16分)
13. ; 14.21 ; 15. ; 16. .
三、解答题(本大题共6小题,共74分)
17.(本题满分13分)
解:(1)甲、乙两卫星各自预报一次,记“甲预报准确”为事件A,“乙预报准确”为事件B.则两卫星只有一颗卫星预报准确的概率为:
… 4分
= 0.8×(1 - 0.75) + (1 - 08)×0.75 = 0.35 …………6分
答:甲、乙两卫星中只有一颗卫星预报准确的概率为0.35 ………7分
(2) 甲独立预报3次,至少有2次预报准确的概率为
…………10分
= =0.896 ………………………12分
答:甲独立预报3次,至少有2次预报准确的概率为0.896. ……… 13分
18.(本题满分13分)
解:(1)∵ …………………2分
= = ……………6分
∴函数 的最小正周期 …………………7分
又由 可得:
的单调递增区间形如: ……9分
(2) ∵ 时, ,
∴ 的取值范围是 ………………11分
∴函数 的最大值是3,最小值是0
从而函数 的是 …………13分
19.(本题满分12分)
解:(1) ∵ ∴由已知条件可得: ,并且 ,
解之得: , ……………3分
从而其首项 和公比 满足: ………5分
故数列 的通项公式为: ……6分
(2) ∵
数列 是等差数列, …………………………8分
∴
=
= = …………………10分
由于 ,当且仅当 最大时, 最大.
所以当 最大时, 或6 …………………………12分
20.(本题满分12分)
解:(1) ∵ 为奇函数 ∴ ………2分
∵ ,导函数 的最小值为-12 ∴ ……3分
又∵直线 的斜率为 ,
并且 的图象在点P 处的切线与它垂直
∴ ,即 ∴ ……………6分
(2) 由第(1)小题结果可得:
……………9分
令 ,得 ……………10分
∵ , ,
∴ 在 [-1, 3]的最大值为11,最小值为-16. ………12分
21.(本题满分12分)
解:(1) ∵函数 有意义的充要条件为
,即是
∴函数 的定义域为 …………3分
∵函数 有意义的充要条件为:
∴函数 的定义域为 …………5分
(2)∵由题目条件知
∴ , …………………7分
∴c的取值范围是:[-5, 5] …………………8分
(3) 即是
∵ 是奇函数,∴ ………………9分
又∵函数 的定义域为 ,并且是增函数
∴ ………………11分
解之得 的取值范围是: = …………12分
22.(本题满分12分)
解:(1) 设双曲线的渐近线方程为 ,即 ,
∵双曲线的渐近线与已知的圆相切,圆心到渐近线的距离等于半径
∴
∴双曲线的渐近线的方程为: ……………2分
又设双曲线的方程为: ,则
∵双曲线的渐近线的方程为 ,且有一个焦点为
∴ , ………………4分
解之得: ,故双曲线的方程是: ……………5分
(2) 联立方程组 ,消去 得: (*)…………6分
∵直线与双曲线C的左支交于两点,方程(*)两根 、 为负数,
∴ …………8分
又∵线段PQ的中点 坐标满足
, ……9分
∴直线 的方程为: ,
即是 ,
直线 在 轴的截距 ……………………11分
又∵ 时, 的取值范围是:
∴直线 的截距 的取值范围是 ……12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com