
题目列表(包括答案和解析)
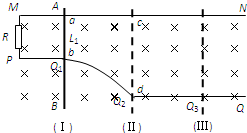 如图所示,两根不计电阻的金属导线MN与PQ 放在水平面内,MN是直导线,PQ的PQ1段是直导线,Q1Q2段是弧形导线,Q2Q3段是直导线,MN、PQ1、Q2Q3相互平行.M、P间接入一个阻值R=0.25Ω的电阻.质量m=1.0kg、不计电阻的金属棒AB能在MN、PQ上无摩擦地滑动,金属棒始终垂直于MN,整个装置处于磁感应强度B=0.5T的匀强磁场中,磁场方向竖直向下.金属棒处于位置(I)时,给金属棒一向右的初速度v1=4 m/s,同时给一方向水平向右F1=3N的外力,使金属棒向右做匀减速直线运动;当金属棒运动到位置(Ⅱ)时,外力方向不变,改变大小,使金属棒向右做匀速直线运动2s到达位置(Ⅲ).已知金属棒在位置(I)时,与MN、Q1Q2相接触于a、b两点,a、b的间距L1=1 m;金属棒在位置(Ⅱ)时,棒与MN、Q1Q2相接触于c、d两点;位置(I)到位置(Ⅱ)的距离为7.5m.求:
如图所示,两根不计电阻的金属导线MN与PQ 放在水平面内,MN是直导线,PQ的PQ1段是直导线,Q1Q2段是弧形导线,Q2Q3段是直导线,MN、PQ1、Q2Q3相互平行.M、P间接入一个阻值R=0.25Ω的电阻.质量m=1.0kg、不计电阻的金属棒AB能在MN、PQ上无摩擦地滑动,金属棒始终垂直于MN,整个装置处于磁感应强度B=0.5T的匀强磁场中,磁场方向竖直向下.金属棒处于位置(I)时,给金属棒一向右的初速度v1=4 m/s,同时给一方向水平向右F1=3N的外力,使金属棒向右做匀减速直线运动;当金属棒运动到位置(Ⅱ)时,外力方向不变,改变大小,使金属棒向右做匀速直线运动2s到达位置(Ⅲ).已知金属棒在位置(I)时,与MN、Q1Q2相接触于a、b两点,a、b的间距L1=1 m;金属棒在位置(Ⅱ)时,棒与MN、Q1Q2相接触于c、d两点;位置(I)到位置(Ⅱ)的距离为7.5m.求:如图所示,两根不计电阻的金属导线MN与PQ 放在水平面内,MN是直导线,PQ的PQ1段是直导线,Q1Q2段是弧形导线,Q2Q3段是直导线,MN、PQ1、Q2Q3相互平行,M、P间接入一个阻值R=0.25Ω的电阻。一根质量为1.0 kg不计电阻的金属棒AB能在MN、PQ上无摩擦地滑动,金属棒始终垂直于MN,整个装置处于磁感应强度B=0.5T的匀强磁场中,磁场方向竖直向下。金属棒处于位置(I)时,给金属棒一个向右的速度v1=4 m/s,同时方向水平向右的外力F1 =3 N作用在金属棒上使金属棒向右做匀减速直线运动;当金属棒运动到位置(Ⅱ)时,外力方向不变,大小变为F2,金属棒向右做匀速直线运动,经过时间t =2 s到达位置(Ⅲ)。金属棒在位置(I)时,与MN、Q1Q2相接触于a、b两点,a、b的间距L1=1 m,金属棒在位置(Ⅱ)时,棒与MN、Q1Q2相接触于c、d两点。已知s1=7.5 m。求:(1)金属棒向右匀减速运动时的加速度大小?
(2)c、d两点间的距离L2=?
(3)外力F2的大小?
(4)金属棒从位置(I)运动到位置(Ⅲ)的过程中,电阻R上放出的热量Q=?

如图所示,两根不计电阻的金属导线MN与PQ 放在水平面内,MN是直导线,PQ的PQ1段是直导线,Q1Q2段是弧形导线,Q2Q3段是直导线,MN、PQ1、Q2Q3相互平行,M、P间接入一个阻值R=0.25Ω的电阻。一根质量为1.0 kg不计电阻的金属棒AB能在MN、PQ上无摩擦地滑动,金属棒始终垂直于MN,整个装置处于磁感应强度B=0.5T的匀强磁场中,磁场方向竖直向下。金属棒处于位置(I)时,给金属棒一个向右的速度v1=4 m/s,同时方向水平向右的外力F1 =3 N作用在金属棒上使金属棒向右做匀减速直线运动;当金属棒运动到位置(Ⅱ)时,外力方向不变,大小变为F2,金属棒向右做匀速直线运动,经过时间t =2 s到达位置(Ⅲ)。金属棒在位置(I)时,与MN、Q1Q2相接触于a、b两点,a、b的间距L1=1 m,金属棒在位置(Ⅱ)时,棒与MN、Q1Q2相接触于c、d两点。已知s1=7.5 m。求:(1)金属棒向右匀减速运动时的加速度大小?
(2)c、d两点间的距离L2=?
(3)外力F2的大小?
(4)金属棒从位置(I)运动到位置(Ⅲ)的过程中,电阻R上放出的热量Q=?
如图所示,两根不计电阻的金属导线MN与PQ放在水平面内,MN是直导线,PQ的PQ1段是直导线,Q1Q2段是弧形导线,Q2Q3段是直导线,MN、PQ1、Q2Q3相互平行,M、P间接入一个阻值R=0.25Ω的电阻。一根质量为1.0 kg不计电阻的金属棒AB能在MN、PQ上无摩擦地滑动,金属棒始终垂直于MN,整个装置处于磁感应强度B=0.5T的匀强磁场中,磁场方向竖直向下。金属棒处于位置(I)时,给金属棒一个向右的速度v1=4 m/s,同时方向水平向右的外力F1 ="3" N作用在金属棒上使金属棒向右做匀减速直线运动;当金属棒运动到位置(Ⅱ)时,外力方向不变,大小变为F2,金属棒向右做匀速直线运动,经过时间t ="2" s到达位置(Ⅲ)。金属棒在位置(I)时,与MN、Q1Q2相接触于a、b两点,a、b的间距L1=1 m,金属棒在位置(Ⅱ)时,棒与MN、Q1Q2相接触于c、d两点。已知s1="7.5" m。求:(1)金属棒向右匀减速运动时的加速度大小?
(2)c、d两点间的距离L2=?
(3)外力F2的大小?
(4)金属棒从位置(I)运动到位置(Ⅲ)的过程中,电阻R上放出的热量Q=?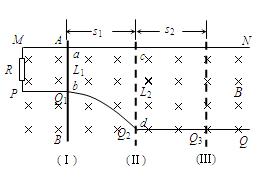
如图所示,两根不计电阻的金属导线MN与PQ 放在水平面内,MN是直导线,PQ的PQ1段是直导线,Q1Q2段是弧形导线,Q2Q3段是直导线,MN、PQ1、Q2Q3相互平行,M、P间接入一个阻值R=0.25Ω的电阻。一根质量为1.0 kg不计电阻的金属棒AB能在MN、PQ上无摩擦地滑动,金属棒始终垂直于MN,整个装置处于磁感应强度B=0.5T的匀强磁场中,磁场方向竖直向下。金属棒处于位置(I)时,给金属棒一个向右的速度v1=4 m/s,同时方向水平向右的外力F1 =3 N作用在金属棒上使金属棒向右做匀减速直线运动;当金属棒运动到位置(Ⅱ)时,外力方向不变,大小变为F2,金属棒向右做匀速直线运动,经过时间t =2 s到达位置(Ⅲ)。金属棒在位置(I)时,与MN、Q1Q2相接触于a、b两点,a、b的间距L1=1 m,金属棒在位置(Ⅱ)时,棒与MN、Q1Q2相接触于c、d两点。已知s1=7.5 m。求:(1)金属棒向右匀减速运动时的加速度大小?
(2)c、d两点间的距离L2=?
(3)外力F2的大小?
(4)金属棒从位置(I)运动到位置(Ⅲ)的过程中,电阻R上放出的热量Q=?
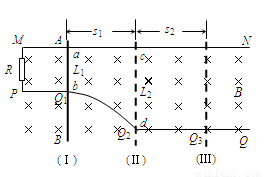
一、选择题(本大题共10小题,每小题5分,共50分)
1~
二、填空题(本大题共6小题,每小题4分,共24分)
11. ; 12 . ; 13. 31;
14. ; 15. ; 16. - ,0 .
三、解答题(本大题共6小题,共76分)
17.(本题满分13分)
解:(Ⅰ)当a=2时,A= , …………………………2分
B= …………………………4分
∴ A B= …………………………6分
(Ⅱ)∵(a2+1)-a=(a- )2+ >0,即a2+1>a
∴B={x|a<x<a2+1} ……………………7分
①当
②当
由B A得: 2≤a≤3 …………………10分
③当
由B A得 -1≤a≤- …………………12分
综上,a的范围为:[-1,- ]∪[2,3] …………………13分
18.(本题满分13分)
解:(Ⅰ)由 ………4分
∵
∴ 的值域为[-1,2] ……………………7分
(Ⅱ)∵
∴
∴ ………………10分
∴ ………………13分
19. (本题满分13分)
解:(Ⅰ) , , ……………………2分
设 与 在公共点 处的切线相同
由题意 ,
即 ……………………4分
由 得: ,或 (舍去)
即有 ……………………6分
(Ⅱ)设 ,……………………7分
则 ……………………9分
x 时 <0,x >0
∴ 在 为减函数,在 为增函数, ……………………11分
于是函数 在 上的最小值是:F(a)=f(a)-g(a)=0 ……………………12分
故当 时,有 ,
所以,当 时, ……………………13分
20. (本题满分13分)
解:(Ⅰ)选取的5只恰好组成完整“奥运吉祥物”的概率
………………5分
(Ⅱ) …………………6分
…………10分
ξ的分布列为:
ξ 10 8 6 4
P
…………13分
21.(本题满分12分)
解:(Ⅰ)∵ , ∴ …………………………1分
由y= 解得: …………………………2分
∴ ………………………3分
(Ⅱ)由题意得: …………………………4分
∴
∴{ }是以 =1为首项,以4为公差的等差数列. …………………………6分
∴ ,∴ . ………………………7分
(Ⅲ)∴ ………8分
则
∴
∴ ,∴ {bn}是一单调递减数列. ………………………10分
∴ ,要使 ,则 ,∴
又kN* ,∴k8 ,∴kmin=8
即存在最小的正整数k=8,使得 ……………………12分
22.(本题满分12分)
解:(Ⅰ)由余弦定理得: ……1分
即16=
= =
所以 ,
即 ……………………………………………4分
(当动点P与两定点A,B共线时也符合上述结论)
所以动点P的轨迹为以A,B为焦点,实轴长为 的双曲线
所以,轨迹G的方程为 …………………………………………6分
(Ⅱ)假设存在定点C(m,0),使 为常数.
①当直线l不与x轴垂直时,设直线l的方程为
…………………………………………7分
由题意知,
设 ,则 , …………………8分
于是
∴
= ………………9分
=
要是使得 为常数,当且仅当 ,此时 ………………11分
②当直线l与x轴垂直时, ,当 时 .
故,在x轴上存在定点C(1,0) ,使得 为常数. …………………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com