查看答案和解析>>

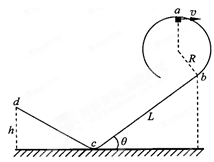
水平轨道与半径R=2m，高为h=0.8m的一段圆弧形光滑轨道连接，如图所示．一个物体从水平轨道上以初速度v₀冲上圆弧轨道并通过最高点而没有脱离轨道，求物体的初速度v₀的范围．

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

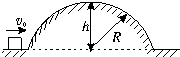
（16分）光滑圆轨道和两倾斜直轨道组成如图所示装置，其中直轨道bc粗糙，直轨道cd光滑，两轨道相接处为一很小的圆弧。质量为m=0.1kg的滑块（可视为质点）在圆轨道上做圆周运动，到达轨道最高点a时的速度大小为v=4m/s，当滑块运动到圆轨道与直轨道bc的相切处b时，脱离圆轨道开始沿倾斜直轨道bc滑行，到达轨道cd上的d点时速度为零。若滑块变换轨道瞬间的能量损失可忽略不计，已知圆轨道的半径为R=0.25m，直轨道bc的倾角θ=37^o，其长度为L=26.25m，d点与水平地面间的高度差为h=0.2m，取重力加速度g=10m/s²，sin37°=0.6。求：

（1）滑块在圆轨道最高点a时对轨道的压力大小；
（2）滑块与直轨道bc问的动摩擦因数；

查看答案和解析>>

1．A  符合机械能守恒条件的只有A项。

2．B  速度为矢量，运算依据平行四边形定则。功是标量。

3．B 

4．C  由动能定律得，所以C项正确。

5．BD 

6．C  两图中物体滑动时摩擦力做功都等于，为AB间的水平距离。

7．ACD 

8．D  从表格中的数据分析得到d增大几倍，s增加几倍的平方，排除AB项；弹力做功转化为摩擦力做功，摩擦力做功之比与s，所以弹力做功正比与s或正比于d²。

9．AD 

10．AD 

11．人与车的总质量m，。

12．3，-18。

13．（1）重力势能的减小量为：J

   （2）重锤下落到B点时的速度为m/s

重锤下落到B点时增加的动能为J

   （3）在实验误差允许的范围内，重锤减小的重力势能等于其动能的增加，验证了机械能守恒定律。重锤减小的重力势能略大于其增加的动能，其原因是重锤在下落时要受到阻力作用（对纸带的摩擦力、空气阻力），必须克服阻力做功，减小的重力势能等于增加的动能加上克服阻力所做的功。

14．（1）天平、刻度尺（2）重力势能、质量、上升高度（3）见下图表

小球的质量m=          kg，弹簧A

压缩量x（m）

上升高度h（m）

E=mgh（J）

压缩量x=          cm，小球的质量m=          Kg

弹簧

A

B

C

劲度系数k（N/m）

上升高度h（m）

E=mgh（J）

15．，

（1）由动能定理得：，即  

（2）设到P点的速度为，绳子所受拉力为F。

Q→P过程，由机械能守恒得：

在P点， ，解得：

16．(1)设最高点A与高低点C之间的高度差为h，则

        h==h₁+h₂==1.2m+0.8m==2m．．．．．．．．．．．．．．．．．．．．．．．．．．．①

        设跳板被压缩到最低点C时的弹性势能为Ep，根据机械能守恒，

        有Ep==mgh．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．②

        E₀==60×10×2J==1.2×10³J．．．．．．．．．．．．．．．．．．．．．．．．．．③

    (2)设最高点与水面之间的高度差为H，则

        H==h₁+h₃==1.2m+3m=4.2m  ．．．．．．．．．．．．．．．．．．．   ④

    运动员做自由落体运动，设运动员入水前的速度为ν，

    则ν==．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．⑤

ν==m／s==2m／s≈9.2m／s．．．．．．．．．⑥

17．没弯管的半径为R

    ⑴当小球恰能到达B点时v_B=0，据机械能守恒定律mgh₁=mgR      ∴h₁=R

⑵当小球恰能到达A点时，设小球经过B点的速度为v₀，  则：v₀t=R   ①

1/2gt²=R ②

mgh₂=mgR+1/2mv₀²  ③

由①②③式得：h₂=5/4R，  ∴ h₁：h₂=4:5

18．⑴假设工件在传送带上一直做匀加速运动，末速度为。

根据动能定理：，解得：

   ∴假设不成立，即工件在传送带上先匀加速，再匀速运动。

⑵∵工件最后随传送带做匀速运动，  ∴末速为

根据动能定理：，解得：