
题目列表(包括答案和解析)
观察是思考的“外壳”,要想思考得好,一定要善于观察.数学家在发现或解决问题时往往首先依赖于他对若干现象的观察--通过观察,如果发现某种值得注意的规律,就对它进行研究,并力图从中发现某种结论,去解释或描述这种模型,以求问题的顺利解决.例如,如果让你用任意方法去切一块圆饼,只要通过同一点不超过两刀,那么最多能得到几块?
自然,我们用不着特地去买一块饼来,只要在纸上画一些圆就行了.我们对各圆进行不同次数的切割,并在表中记录结果,得到:

我们仔细考查一下这张表,看看能否找到其中的规律.从记录上看,增加的块数分别是自然数1,2,3.切割次数也分别是1,2,3.这种规律是否继续有效呢?让我们再多试几次,并记录数据,得到:

现在的增加数分别是1,2,3,4,5,可见规律继续有效.这种规律使我们预测到:切割6次得22块,切割7次得29块.并进一步能使我们预测切割任意次所得的块数.
想一想:切割8次、9次将分别得到多少块?
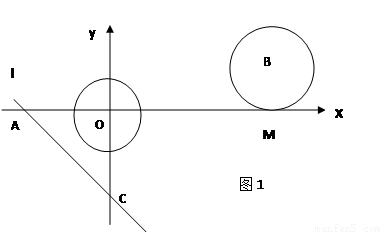
如图1,在平面直角坐标系中,以坐标原点O为圆心的⊙O的半径为![]() -1,直线l y=-X-
-1,直线l y=-X-![]() 与坐标轴分别交于A,C两点,点B的坐标为(4,1) ,⊙B与X轴相切于点M.
与坐标轴分别交于A,C两点,点B的坐标为(4,1) ,⊙B与X轴相切于点M.
(1) 求点A的坐标及∠CAO的度数;
(2) ⊙B以每秒1个单位长度的速度沿X轴负方向平移,同时,直线l绕点A顺时针匀速旋转.当⊙B第一次与⊙O相切时,直线l也恰好与⊙B第一次相切.问:直线AC绕点A每秒旋转多少度?
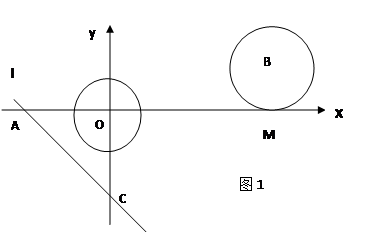
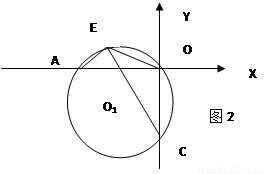
(3)如图2.过A,O,C三点作⊙O1,点E是劣弧![]() 上一点,连接EC,EA.EO,当点E在劣弧
上一点,连接EC,EA.EO,当点E在劣弧![]() 上运动时(不与A,O两点重合),
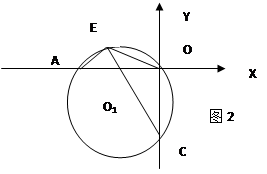
上运动时(不与A,O两点重合),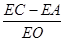 的值是否发生变化?如果不变,求其值,如果变化,说明理由.
的值是否发生变化?如果不变,求其值,如果变化,说明理由.
 .
.
【解析】(1)已知点A,C的坐标,故可推出OA=OC,最后可得∠CAO=45°.
(2)依题意,设⊙B平移t秒到⊙B1处与⊙O第一次相切,连接B1O,B1N,则MN=3.连接B1A,B1P可推出∠PAB1=∠NAB1.又因为OA=OB1=![]() ,故∠AB1O=∠NAB1,∠PAB1=∠AB1O继而推出PA∥B1O.然后在Rt△NOB1中∠B1ON=45°,∴∠PAN=45°得出∠1=90°.然后可得直线AC绕点A平均每秒30度.
,故∠AB1O=∠NAB1,∠PAB1=∠AB1O继而推出PA∥B1O.然后在Rt△NOB1中∠B1ON=45°,∴∠PAN=45°得出∠1=90°.然后可得直线AC绕点A平均每秒30度.
(3)在CE上截取CK=EA,连接OK,证明△OAE≌△OCK推出OE=OK,∠EOA=∠KOC,∠EOK=∠AOC=90°.最后可证明![]()
如图1,在平面直角坐标系中,以坐标原点O为圆心的⊙O的半径为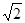 -1,直线l y=-X-
-1,直线l y=-X-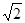 与坐标轴分别交于A,C两点,点B的坐标为(4,1) ,⊙B与X轴相切于点M.
与坐标轴分别交于A,C两点,点B的坐标为(4,1) ,⊙B与X轴相切于点M.
(1) 求点A的坐标及∠CAO的度数;
(2) ⊙B以每秒1个单位长度的速度沿X轴负方向平移,同时,直线l绕点A顺时针匀速旋转.当⊙B第一次与⊙O相切时,直线l也恰好与⊙B第一次相切.问:直线AC绕点A每秒旋转多少度?
(3)如图2.过A,O,C三点作⊙O1
,点E是劣弧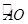 上一点,连接EC,EA.EO,当点E在劣弧
上一点,连接EC,EA.EO,当点E在劣弧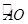 上运动时(不与A,O两点重合),
上运动时(不与A,O两点重合),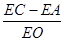 的值是否发生变化?如果不变,求其值,如果变化,说明理由.
的值是否发生变化?如果不变,求其值,如果变化,说明理由.
 .
.
【解析】(1)已知点A,C的坐标,故可推出OA=OC,最后可得∠CAO=45°.
(2)依题意,设⊙B平移t秒到⊙B1处与⊙O第一次相切,连接B1O,B1N,则MN=3.连接B1A,B1P可推出∠PAB1=∠NAB1.又因为OA=OB1=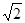 ,故∠AB1O=∠NAB1,∠PAB1=∠AB1O继而推出PA∥B1O.然后在Rt△NOB1中∠B1ON=45°,∴∠PAN=45°得出∠1=90°.然后可得直线AC绕点A平均每秒30度.
,故∠AB1O=∠NAB1,∠PAB1=∠AB1O继而推出PA∥B1O.然后在Rt△NOB1中∠B1ON=45°,∴∠PAN=45°得出∠1=90°.然后可得直线AC绕点A平均每秒30度.
(3)在CE上截取CK=EA,连接OK,证明△OAE≌△OCK推出OE=OK,∠EOA=∠KOC,∠EOK=∠AOC=90°.最后可证明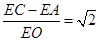
小程买80分邮票和1元邮票共花了16元,已知所买的一元邮票比80分邮票少2枚,设买了80分邮票x枚,则依题意得到的方程是
[ ]
小明买80分邮票与1元邮票共花了16元,已知所买的1元邮票比80分邮票少2枚,设买了80分邮票x枚,依据题意得到的方程是( )
A
.0.8x+(x-2)=16 B.0.8x+(x+2)=16C
.80x+(x-2)=16 D.80x+(x+2)=16湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com