题目列表(包括答案和解析)
如图13所示，在光滑的水平面上有一长为L的木板B，上表面粗糙，在其左端有一光滑的1/4圆弧槽C，与长木板接触但不相连，圆弧槽的下端与木板上表面相平，B、C静止在水平面上。现有滑块A以初速V0从右端滑上B，并以1/2 V0滑离B，确好能到达C的最高点。A、B、C的质量均为m，试求：（1）木板B上表面的动摩擦因素μ；（2）1/4圆弧槽C的半径R；（3）当A滑离C时，C的速度。
如图所示，在光滑的水平面上，质量分别为m1和m2的木块A和B之间用轻弹簧相连，在拉力F作用下，以加速度a做匀加速直线运动，某时刻突然撤去拉力F，此瞬时A和B的加速度为a1和a2，则( )
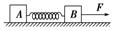
图3－3－13
A．a1＝a2＝0
B．a1＝a，a2＝0
C．a1＝a，a2＝a
D．a1＝a，a2＝－a
【解析】：选D.两物体在光滑的水平面上一起以加速度a向右匀加速运动时，弹簧的弹力F弹＝m1a，在力F撤去的瞬间，弹簧的弹力来不及改变，大小仍为m1a，因此对A来讲，加速度此时仍为a，对B物体：取向右为正方向，－m1a＝m2a2，a2＝－a，所以只有D项正确．
如图13所示，在直角三角形ACD所包围的区域内存在垂直纸面向外的水平匀强磁场．AC边竖直．CD边水平，且边长AC=2CD=2d，在该磁场的右侧
处有一对竖直放 置的平行金属板MN，两板问的距离为L．在板中央各有一个小孔O1、O2，O1、O??2在同一水平直线上，与平行金属板相接的是两条竖直放置的间距也为L的足够长光滑金属导轨，导轨处在水平向里的匀强磁场中，磁感应强度为B，导体棒PQ与导轨接触良好，与阻值为R的电阻形成闭合回路（导轨的电阻不计），整个装置处在真空室中。有一束电荷量为+q，质量为m的粒子流（重力不计），以速率v0从CD边中点竖直向上射人磁场区域，射出磁场后能沿O1O2方向进人两平行金属板间并能从O??2孔射出。现由静止释放导体棒PQ．其下滑一段距离后开始匀速运动。此后粒子恰好不能从O2孔射出，而能返回后从磁场的AD边射出，假设返回的粒子与入射粒子不会相撞。求：
（1）在直角三角形ACD内磁场的磁感应强度B。。
（2）导体棒PQ的质量M。
（3）带电粒子从CD边进入磁场到从AD边射出磁场所用的时间
图13 图14
图13
（1）金属杆达到的最大速度vm;
（2）在这2 s时间内回路产生的热量Q；
（3）当速度变为5 m/s 时，金属杆的加速度a.
14
15
16
17
18
19
20
21
BC
A
C
D
C
CD
AC
C
三.实验题答案:
22.(一) （1）将小木块从斜板上A点由静止释放，运动至水平板上B点静止；
（2）用图钉把细线拉紧固定在A，B两点间；
（3）用量角器测量细线与水平板间的夹角θ；
（4）动摩擦因数表示为μ=tanθ
（二） (1) 
(2)
U/、U分别为V/、V的读数
四.计算题答案:
25（20分）. （1）
∴
(6分)
（2）
(6分)
（3）∵
∴
（2分）
(6分)
23（16分）． (1)单摆的周期
＝2s (2分)
N次全振动的时间 t＝NT＝
＝20s (2分)
木箱在这段时间内的位移 S＝vt =NTv=
＝
(2)绳子对铁球的拉力 T＝mg/cos37° （2分）
球受到的合力 F1＝mgtan37° （l分）
根据牛顿定律，球的加速度a＝F1/m＝gtan37°球相对箱静止，箱的加速度也为此值 （2分）
绳对箱的拉力的竖直向下分力Ty＝Tcos37°＝mg （2分）
箱子在竖直方向的合力为0，故地面对箱的支持力N＝(M+m) g (1分)
绳对箱的拉力的水平向左的分力Tx＝Tsin37°＝mgtan37° （1分）
设推力大小为 F.则箱受到的合力∑F＝F-Tx-μN =Ma，得
F=Ma+TX+μN=(M+m)(μ+tan37°)g＝51N (1分)
（用整体法求出推力大小同样给分）
24（18分）. （1）当A在B上滑动时，A与BC整体发生作用，由于水平面光滑，A与BC组成的系统动量守恒，
，（2分） 得
（1分）
系统动能的减小量等于滑动过程中产生的内能， 
，（1分）
，（2分）
得
（1分）
（2）当A滑上C，B与C分离，A与C发生作用，设到达最高点时速度相等为V2，由于水平面光滑，A与C组成的系统动量守恒， 
，（2分）得
A与C组成的系统机械能守恒，
（2分）
得
（1分）
（3）当A滑下C时，设A的速度为VA，C的速度为VC，A与C组成的系统动量守恒，
, （2分）
A与C组成的系统动能守恒，
（2分）
得VC = 
（2分）
化学答案DDACDBBC
26．（1）
C
N
O
Al
Cl
K
Fe
(2)
（3）（写出其中2个即给分，如多写了B等元素，不给分也不扣分）
|
0.1mol
（2分）
(2分)
(2分)
(2分)
2CuO CH3CH2OH+CuO
CH3CHO+Cu+H2O 
⑷乙酸 c 蒸馏