题目列表(包括答案和解析)
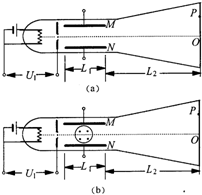如图（a）所示的真空管中，电子从灯丝K发出 （初速不计），经电压为U1的加速电场加速后沿中心线进入两平行金属板M，N间的匀强电场中，通过电场后打到荧光屏上的P点处，设M，N板间电压为U2，两板距离为d，板长为Ll，板右端到荧光屏的距离为L2，已知U1=576V，U2=168V，L1=6cm，d=3cm，L2=21cm，电子的比荷| e | m |
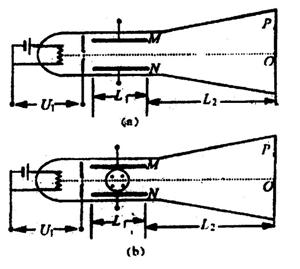
如图（a）所示的真空管中，电子从灯丝K发出（初速不计），经电压为U1的加速电场加速后沿中心线进入两平行金属板M、N间的匀强电场中，通过电场后打到荧光屏上的P点处，设M、N板间电压为U2，两板距离为d，板长为L1，板右端到荧光屏的距离为L2，已知U1=576V，U2=168V，L1=6cm，d=3cm，L2=21cm，电子的比荷
C/kg，求：（1）电子离开偏转电场时的偏角θ（即电子离开偏转电场时速度与进入偏转电场时速度的夹角）；
（2）电子打到荧光屏上的位置P偏离荧光屏中心O的距离OP；
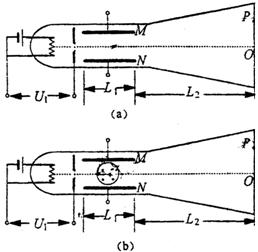（3）若撤去M、N间的电压U2，而在两平行板中的圆形区域内（如图b所示）加一磁感应强度为B=0.001T的匀强磁场，圆形区域的中心正好就是两平行板空间部分的中心，要使电子通过磁场后仍打在荧光屏上的P点处，圆形区域的半径r为多少？（结果中可含有反三角函数）
，求：
的加速电场加速后沿中心线进入两平行金属板M、N间的匀强电场中，通过电场后打到荧光屏上的P点处，设M、N板间电压为
，两极距离为d，板长为
板右端到荧光屏的距离为
，已知
，电子的比荷
，求：
（即电子离开偏转电场时速度与进入偏转电场时速度的夹角）。而在两平行板中的圆形区域内（如图b所示）加一磁感应强度为B=0.001T的匀强磁场，圆形区域的中心正好就是两平行板空间部分的中心。要使电子通过磁场后仍打在荧光屏上的P点处，圆形区域的半径r为多少？（结果中可含有反三角函数）
在如图所示的真空管的，光照射到金属钠电极K上，如果有光电子逸出时就会奔向阳极A，从而在电路中形成电流，G表就会偏转．在研究光电效应的实验中，用某种频率的单色光a照射真空管钠电极K时，电流计G的指针发生偏转，而用另一频率的单色光b照射真空管钠电极K时，电流计G的指针不发生偏转，那么（ ）14
15
16
17
18
19
20
21
BC
A
C
D
C
CD
AC
C
三.实验题答案:
22.(一) （1）将小木块从斜板上A点由静止释放，运动至水平板上B点静止；
（2）用图钉把细线拉紧固定在A，B两点间；
（3）用量角器测量细线与水平板间的夹角θ；
（4）动摩擦因数表示为μ=tanθ
（二） (1) 
(2)
U/、U分别为V/、V的读数
四.计算题答案:
25（20分）. （1）
∴
(6分)
（2）
(6分)
（3）∵
∴
（2分）
(6分)
23（16分）． (1)单摆的周期
＝2s (2分)
N次全振动的时间 t＝NT＝
＝20s (2分)
木箱在这段时间内的位移 S＝vt =NTv=
＝
(2)绳子对铁球的拉力 T＝mg/cos37° （2分）
球受到的合力 F1＝mgtan37° （l分）
根据牛顿定律，球的加速度a＝F1/m＝gtan37°球相对箱静止，箱的加速度也为此值 （2分）
绳对箱的拉力的竖直向下分力Ty＝Tcos37°＝mg （2分）
箱子在竖直方向的合力为0，故地面对箱的支持力N＝(M+m) g (1分)
绳对箱的拉力的水平向左的分力Tx＝Tsin37°＝mgtan37° （1分）
设推力大小为 F.则箱受到的合力∑F＝F-Tx-μN =Ma，得
F=Ma+TX+μN=(M+m)(μ+tan37°)g＝51N (1分)
（用整体法求出推力大小同样给分）
24（18分）. （1）当A在B上滑动时，A与BC整体发生作用，由于水平面光滑，A与BC组成的系统动量守恒，
，（2分） 得
（1分）
系统动能的减小量等于滑动过程中产生的内能， 
，（1分）
，（2分）
得
（1分）
（2）当A滑上C，B与C分离，A与C发生作用，设到达最高点时速度相等为V2，由于水平面光滑，A与C组成的系统动量守恒， 
，（2分）得
A与C组成的系统机械能守恒，
（2分）
得
（1分）
（3）当A滑下C时，设A的速度为VA，C的速度为VC，A与C组成的系统动量守恒，
, （2分）
A与C组成的系统动能守恒，
（2分）
得VC = 
（2分）
化学答案DDACDBBC
26．（1）
C
N
O
Al
Cl
K
Fe
(2)
（3）（写出其中2个即给分，如多写了B等元素，不给分也不扣分）
|
0.1mol
（2分）
(2分)
(2分)
(2分)
2CuO CH3CH2OH+CuO
CH3CHO+Cu+H2O 
⑷乙酸 c 蒸馏