
题目列表(包括答案和解析)
定义:已知函数f(x)与g(x),若存在一条直线y=kx +b,使得对公共定义域内的任意实数均满足g(x)≤f(x)≤kx+b恒成立,其中等号在公共点处成立,则称直线y=kx +b为曲线f(x)与g(x)的“左同旁切线”.已知
(I)证明:直线y=x-l是f(x)与g(x)的“左同旁切线”;
(Ⅱ)设P(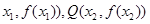 是函数 f(x)图象上任意两点,且0<x1<x2,若存在实数x3>0,使得
是函数 f(x)图象上任意两点,且0<x1<x2,若存在实数x3>0,使得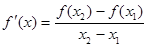 .请结合(I)中的结论证明:
.请结合(I)中的结论证明: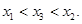
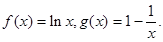
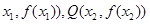 是函数 f(x)图象上任意两点,且0<x1<x2,若存在实数x3>0,使得
是函数 f(x)图象上任意两点,且0<x1<x2,若存在实数x3>0,使得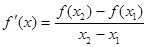 .请结合(I)中的结论证明:
.请结合(I)中的结论证明: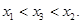
| |||||
| |||||
 与
与 都是非零向量,则“
都是非零向量,则“ ”是“
”是“ ”的充要条件;②已知等腰△ABC的腰为底的2倍,则顶角A的正切值是
”的充要条件;②已知等腰△ABC的腰为底的2倍,则顶角A的正切值是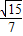 ;③在平面直角坐标系xoy中,四边形ABCD的边AB∥DC,AD∥BC,已知点A(-2,0),B(6,8),C(8,6),则D点的坐标为(0,-1);④设
;③在平面直角坐标系xoy中,四边形ABCD的边AB∥DC,AD∥BC,已知点A(-2,0),B(6,8),C(8,6),则D点的坐标为(0,-1);④设 ,
, ,
, 为同一平面内具有相同起点的任意三个非零向量,且满足
为同一平面内具有相同起点的任意三个非零向量,且满足 与
与 不共线,
不共线, ⊥
⊥ ,|
,| |=|
|=| |,则|
|,则| •
• |的值一定等于以
|的值一定等于以 ,
, 为邻边的平行四边形的面积.其中正确命题的序号是 .(写出全部正确结论的序号)
为邻边的平行四边形的面积.其中正确命题的序号是 .(写出全部正确结论的序号)必做部分
1. 2.
2. 3.
3. 4.2.6 5.
4.2.6 5. 6.640+80π 7.
6.640+80π 7. 8.①④ 9.
8.①④ 9. 10.
10.
11.“ ,使得
,使得 且
且 ” 12.
” 12. 13.6 14.9
13.6 14.9
(12.图13.作 则
则 因
因 ,故
,故 ,
, )
)
15.(1)取AB的中点G,则易证得A1G∥D1F.
又正方形A1ABB1中,E、G分别是相应边的中点,
∴A1G⊥AE,∴D1F⊥AE.
(2)由正方体可知:A1 D1⊥面A1ABB1,∴A1D1⊥AE .
又由(1)已证:D1F⊥AE.
∵A1D1∩D1F= D1,∴AE⊥平面A1FD1 .
又 平面AED,∴平面AED⊥平面A1FD1 .
平面AED,∴平面AED⊥平面A1FD1 .
16.(1)全班32名学生中,有15名女生,17名男生.在伪代码中,根据“S←S/15,T←T/17”可以推知,“k=1”和“k=0”分别代表男生和女生;S,T,A分别代表女生、男生及全班成绩的平均分;横线①处应填“(S+T)/32”.
(2)女生、男生及全班成绩的平均分分别为S=78,T=76.88,A≈77.4.
(3)15名女生成绩的平均分为78,17名男生成绩的平均分为77.88.从中可以看出女生成绩比较集中,整体水平稍高于男生;男生中的高分段比女生高,低分段比女生多,相比较男生两极分化比较严重.
17.(1)

 .
. ,
, 由题意可知
由题意可知
解得 .
.
(2)由(Ⅰ)可知 的最大值为1,
的最大值为1, .
.
 ,
, . 而
. 而 ,
,
 .
.
由余弦定理知 ,
,
 ,联立解得
,联立解得
 .
.
18.(1)设A、B两点的坐标分别为 得
得 , 根据韦达定理,得
, 根据韦达定理,得
∴线段AB的中点坐标为( ).
).
由已知得
故椭圆的离心率为 .
.
(2)由(1)知 从而椭圆的右焦点坐标为
从而椭圆的右焦点坐标为 设
设 关于直线
关于直线 :
: 的对称点为
的对称点为 解得
解得 .由已知得
.由已知得  ,故所求的椭圆方程为
,故所求的椭圆方程为 .
.
19.(1)方法一: .由题设,得
.由题设,得 , ①
, ①
 .
②
.
②
∵ ,∴
,∴ ,∴
,∴ .
.
由①代入②得 ,∴
,∴ ,
,
得 ∴
∴ 或
或 .
③
.
③
将 代入
代入 中,得
中,得 . ④
. ④
由③、④得 ;
;
方法二:∵ ,∴
,∴ ,∴
,∴ .
.
同上可得 将(1)变为
将(1)变为 代入(2)可得
代入(2)可得  ,所以
,所以 ,则
,则 .
.
方法三:同上可得 将(1)变为
将(1)变为 代入(2)可得
代入(2)可得 ,显然
,显然 ,所以
,所以 .
.
因为 图象的开口向下,且有一根为x1=1,
图象的开口向下,且有一根为x1=1,
由韦达定理得 ,
, .
.
 ,所以
,所以 ,即
,即 ,则
,则 ,
,
由 得
得  ,所以
,所以  .
.
(2)由(1)知, 的判别式Δ=
的判别式Δ=
∴方程 有两个不等的实根
有两个不等的实根 ,
,
又 ,∴
,∴ ,
,
∴当 或
或 时,
时, ;当
;当 时,
时, .
.
∴函数 的单调增区间是
的单调增区间是 ,
,  .
.
由 知
知 .
.
∵函数 在区间
在区间 上单调递增,∴
上单调递增,∴ ,
,
∴ ,即
,即 的取值范围是
的取值范围是 .
.
(3)由 ,即
,即 ,∵
,∵ ,
,

 ,∴
,∴ ,∴
,∴ 或
或 .(自注:视为
.(自注:视为 的一次函数)
的一次函数)
由题意,得 ,∴
,∴ .
.
∴存在实数 满足条件,即
满足条件,即 的最小值为
的最小值为 .
.
20.(1)由于 ,则
,则 ,
,
∴ ,∴
,∴ .
.
(2)由于 ,由(1)
,由(1) ,则
,则 ,
, ,
,
而 ,则
,则 ,∴
,∴ ;
;
又 ,
,
∴
 .
.
 ,
,
∴ .
.
而 ,且
,且 ,故
,故 , ∴
, ∴ ,因此
,因此 .
.
从而
选做部分
1. (1)设事件 表示“甲选做14题”,事件
表示“甲选做14题”,事件 表示“乙选做14题”,则甲、乙2名学生选做同一道题的事件为“
表示“乙选做14题”,则甲、乙2名学生选做同一道题的事件为“ ”,且事件
”,且事件 、
、 相互独立.
相互独立.
∴  =
= .
.
(2)随机变量 的可能取值为0,1,2,3,4.且
的可能取值为0,1,2,3,4.且 .
.
∴  .
.
所以变量 的分布列为:
的分布列为:

0
1
2
3
4






 . (或
. (或 )
)
2.以A为原点, 分别为x轴,y轴,z轴的正向建立空间直角坐标系A-xyz,则有
分别为x轴,y轴,z轴的正向建立空间直角坐标系A-xyz,则有
D(0,3,0)、D1(0,3,2)、E(3,0,0)、F(4,1,0)、C1(4,3,2).
于是  ,
, .
.
(1)设EC1与FD1所成角为b,则 .
.
(2)设向量 与平面C1DE垂直,则有
与平面C1DE垂直,则有
 .
.
∴ 其中z>0.
其中z>0.
取n0=(-1,-1,2),则n0是一个与平面C1DE垂直的向量.
∵向量 =(0,0,2)与平面CDE垂直,
=(0,0,2)与平面CDE垂直,
∴n0与 所成的角θ为二面角C-DE-C1的平面角.
所成的角θ为二面角C-DE-C1的平面角.
∵ ,∴
,∴ .
.
3.(1)设M= ,则
,则
 =8
=8 =
= ,故
,故

 =
= ,故
,故
联立以上两方程组解得a=6,b=2,c=4,d=4,故M= .
.
(2)由(1)知,矩阵M的特征多项式为 ,故其另一个特征值为
,故其另一个特征值为 .设矩阵M的另一个特征向量是e2
.设矩阵M的另一个特征向量是e2 ,则M e2=
,则M e2= ,解得
,解得 .
.
(3)设点 是直线
是直线 上的任一点,其在矩阵M的变换下对应的点的坐标为
上的任一点,其在矩阵M的变换下对应的点的坐标为 ,则
,则

 =
= ,即
,即 ,
,
代入直线 的方程后并化简得
的方程后并化简得 ,即
,即 .
.
4.(1)抛物线焦点为(1,0).
设 :
: 消去x得
消去x得
 ,
,
则 ,
,

= .
.
(2)设 :
: 消去x,得
消去x,得 .
.
 ,则y1+y2=4t ,y1y2=-4b.
,则y1+y2=4t ,y1y2=-4b.

= .
.
令 ,∴直线l过定点(2,0).
,∴直线l过定点(2,0).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com