
题目列表(包括答案和解析)
 子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?
子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?| 2.52-0.72 |
| B | 2 1 |
答案:(1)如图
(2)答:这条船继续前进,没有被浅滩阻碍的危险。
解:作CD⊥直线AB于点D,
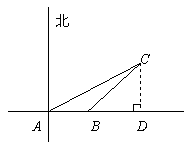 由已知可得∠CAD=30°, ∠CBD=45°,
由已知可得∠CAD=30°, ∠CBD=45°,
AB=100米。
设CD=![]() 米。
米。
在Rt△ACD中
tan∠CAD=![]()
∴AD=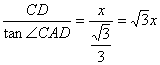
在Rt△CBD中
∵∠CBD=45°, ∴BD=CD=x,
∵AD-BD=AB, ∴![]() 。
。
解得![]()
∴这条船继续前进没有被浅滩阻碍的危险。
| (x1-x2)2+(y1-y2)2 |
| (x1-x2)2+(y1-y2)2 |
| 6 |
| 7 |
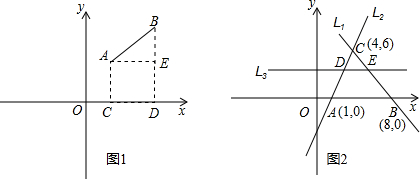
小明和同桌小聪在课后复习时,对课本“目标与评定”中的一道思考题,进行了认真的探索。
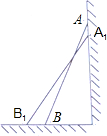
【思考题】如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?
(1)请你将小明对“思考题”的解答补充完整:
解:设点B将向外移动x米,即BB1=x,
则B1C=x+0.7,A1C=AC﹣AA1=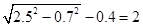
而A1B1=2.5,在Rt△A1B1C中,由 得方程 ,
得方程 ,
解方程得x1= ,x2= ,
∴点B将向外移动 米。
(2)解完“思考题”后,小聪提出了如下两个问题:
【问题一】在“思考题”中,将“下滑0.4米”改为“下滑0.9米”,那么该题的答案会是0.9米吗?为什么?
【问题二】在“思考题”中,梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离,有可能相等吗?为什么?
请你解答小聪提出的这两个问题。
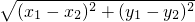 ,下面我们来证明这个公式:证明:如图1,过A点作X轴的垂线,垂足为C,则C点的横坐标为x1,过B点作X轴的垂线,垂足为D,则D点的横坐标为x2,过A点作BD的垂线,垂足为E,则E点的横坐标为x2,纵坐标为y1.∴|AE|=|CD|=|x1-x2|
,下面我们来证明这个公式:证明:如图1,过A点作X轴的垂线,垂足为C,则C点的横坐标为x1,过B点作X轴的垂线,垂足为D,则D点的横坐标为x2,过A点作BD的垂线,垂足为E,则E点的横坐标为x2,纵坐标为y1.∴|AE|=|CD|=|x1-x2|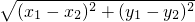 (因为|AB|表示线段长,为非负数)
(因为|AB|表示线段长,为非负数) ,求线段|DA|的长.
,求线段|DA|的长.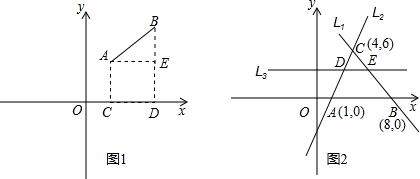
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com