
题目列表(包括答案和解析)
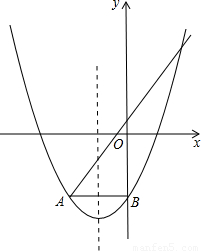
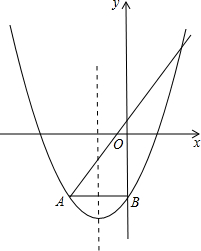
抛物线![]() 与直线y=x+1交于A、C两点,与y轴交于B,AB∥x轴,且
与直线y=x+1交于A、C两点,与y轴交于B,AB∥x轴,且![]()
(1)求抛物线的解析式。
(2)P为x轴负半轴上一点,以AP、AC为边作![]() ,是否存在P,使得Q点恰好在此抛物线上?若存在,请求出P、Q的坐标;若不存在,请说明理由。
,是否存在P,使得Q点恰好在此抛物线上?若存在,请求出P、Q的坐标;若不存在,请说明理由。
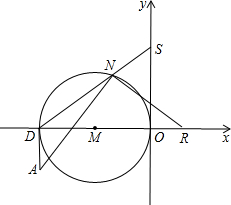
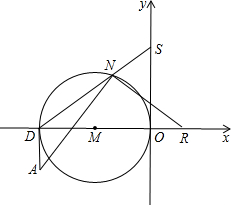
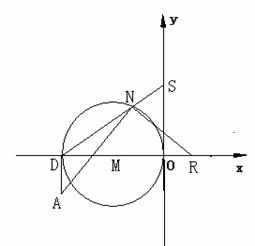 (3)AD⊥X轴于D,以OD为直径作⊙M,N为⊙M上一动点,(不与O、D重合),过N作AN的垂线交x轴于R点,DN交Y轴于点S,当N点运动时,线段OR、OS是否存在确定的数量关系?写出证明。
(3)AD⊥X轴于D,以OD为直径作⊙M,N为⊙M上一动点,(不与O、D重合),过N作AN的垂线交x轴于R点,DN交Y轴于点S,当N点运动时,线段OR、OS是否存在确定的数量关系?写出证明。
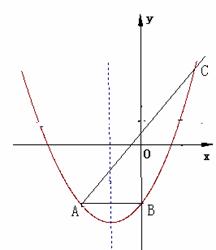
抛物线y=ax2+2ax+b与直线y=x+1交于A、C两点,与y轴交于B,AB∥x轴,且S△ABC=3,(1)求抛物线的解析式.
(2)P为x轴负半轴上一点,以AP、AC为边作![]() CAPQ,是否存在P,使得Q点恰好在此抛物线上?若存在,请求出P、Q的坐标;若不存在,请说明理由.
CAPQ,是否存在P,使得Q点恰好在此抛物线上?若存在,请求出P、Q的坐标;若不存在,请说明理由.
(3)AD⊥X轴于D,以OD为直径作⊙M,N为⊙M上一动点,(不与O、D重合),过N作AN的垂线交x轴于R点,DN交Y轴于点S,当N点运动时,线段OR、OS是否存在确定的数量关系?写出证明.

1-6:CCABAD 7――12:BBDACC
13.7 14. 15.
15. 16.-4 17.
16.-4 17.
18.x-2
19. 证明:如图,因为 AB∥CN
 所以
所以  在
在 和
和 中
中

 ≌
≌


 是平行四边形
是平行四边形
20.(1) (2)500
(2)500
21.(1)(-1,4), ;(2)
;(2) ;
;
(3)直线 与
与 轴的交点B(4,0),与
轴的交点B(4,0),与 轴交于点C(0,8),
轴交于点C(0,8),
绕P(-1,0)顺时针旋转90°后的对应点 (-1, -5),
(-1, -5), (7,-1),
(7,-1),
设直线 的函数解析式为
的函数解析式为 ,
,
22.略(2)
23. 的整数
的整数
(2) 得
得 ,当x=24时,利润最大是3880
,当x=24时,利润最大是3880
24.解:(1)BE=AD
证明:∵△ABC与△DCE是等边三角形
∴∠ACB=∠DCE=60° CA=CB,CE=CD
∴∠BCE=∠ACD ∴△BCE≌△ACD
∴ BE=AD(也可用旋转方法证明BE=AD)
(2)设经过x秒重叠部分的面积是 ,如图在△CQT中
,如图在△CQT中
∵∠TCQ=30° ∠RQP=60°
 ∴∠QTC=30° ∴∠QTC=∠TCQ ∴QT=QC=x∴ RT=3-x
∴∠QTC=30° ∴∠QTC=∠TCQ ∴QT=QC=x∴ RT=3-x
∵∠RTS+∠R=90° ∴∠RST=90°
由已知得 ×32 -
×32 - (3-x)2=
(3-x)2=
x =1,x
=1,x =5,因为0≤x≤3,所以x=1
=5,因为0≤x≤3,所以x=1
答:经过1秒重叠部分的面积是
(3)C′N?E′M的值不变
证明:∵∠ACB=60°∴∠MCE′+∠NCC′=120°
∵∠CNC′+∠NCC′=120° ∴∠MCE′=∠CNC′
∵∠E′=∠C′ ∴△E′MC∽△C′CN
∴ ∴C′N?E′M=C′C?E′C=
∴C′N?E′M=C′C?E′C= ×
× =
=
25.(1)
(2)联立 得A(-2,-1)C(1,2)
得A(-2,-1)C(1,2)
设P(a,0),则Q(4+a,2)
∴
∴
∴Q(-3,2)或(1,2)
(3)∵△AND~△RON,∴
∵△ONS~△DNO,∴
∴
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com