（本小题满分12分）

某研究机构为了研究人的体重与身高之间的关系,随机抽测了20人,得到如下数据:

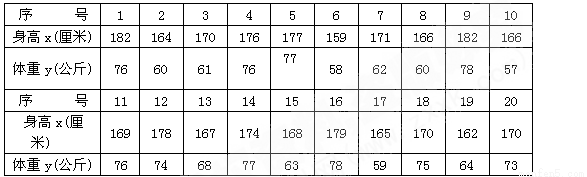
(1)若“身高大于175厘米”的为 “高个”，“身高小于等于175厘米”的为“非高个”；“体重大于75(公斤)”的为“胖子”，“体重小于等于75(公斤)”的为“非胖子”.请根据上表数据完成下面的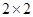联列表:

(2)根据题(1)中表格的数据,若按99%的可靠性要求,能否认为体重与身高之间有关系?

（本小题满分12分）

某研究机构对高三学生的记忆力x和判断力y进行统计分析，得下表数据

（Ⅰ）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程y＝bx＋a；

（Ⅱ）试根据（Ⅰ）求出的线性回归方程，预测记忆力为9的同学的判断力．

                        （相关公式：b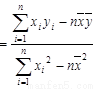，a）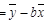

（本小题满分12分）某工艺品加工厂准备生产具有收藏价值的奥运会标志——“中国印·舞动的北京”和奥运会吉祥物——“福娃”．该厂所用的主要原料为A、B两种贵金属，已知生产一套奥运会标志需用原料A和原料B的量分别为4盒和3盒，生产一套奥运会吉祥物需用原料A和原料B的量分别为5盒和10盒．若奥运会标志每套可获利700元，奥运会吉祥物每套可获利1200元，该厂月初一次性购进原料A、B的量分别为200盒和300盒．问该厂生产奥运会标志和奥运会吉祥物各多少套才能使该厂月利润最大？最大利润为多少？

（本小题满分12分）

    某计算机程序每运行一次都随机出现一个二进制的六位数，其中 的各位数中，，（2，3，4，5）出现0的概率为，出现1的概率为，记，当该计算机程序运行一次时，求随机变量X的分布列和数学期望．         

（本小题满分12分）某饮料公司招聘了一名员工，现对其进行一项测试，以使确定工资级别，公司准备了两种不同的饮料共8杯，其颜色完全相同，并且其中4杯为A饮料，另外4杯为B饮料，公司要求此员工一一品尝后，从8杯饮料中选出4杯A饮料，若4杯都选对，则月工资定为3500元，若4杯选对3杯，则月工资定为2800元，否则月工资定为2100元，令X表示此人选对A饮料的杯数，假设此人对A和B两种饮料没有鉴别能力．

（1）求X的分布列；

（2）求此员工月工资的期望.