2,4,6
二、填空题
13．
14．3
15．－192 16． 22.2
三、解答题
17．解：（1）∵
∴
①……………………2分
∴
∴
②……………………4分
联立①，②解得：
……………………6分
（2）
……………………10分
∴
……………………11分
当
此时
……………………12分
18．解：以D1为原点，D1A1所在直线为x轴，D1C1所在直线为y轴，D1D所在直线为z轴建立空间直角坐标系，
则D1（0，0，0），A1（2，0，0），B1（2，2，0），C1（0，2，0），D（0，0，2），A（2，0，2），B（2，2，2），C（0，2，2）P（1，1，4）………………2分
（1）∵
∴
∴PA⊥B1D1.…………………………4分
（2）平面BDD1B1的法向量为
……………………6分
设平面PAD的法向量
，则n⊥
∴
∴
…………………………10分
设所求锐二面角为
，则
……………………12分
19．解：（1）从50名教师随机选出2名的方法数为
选出2人使用版本相同的方法数为
故2人使用版本相同的概率为：
…………………………5分
（2）∵
，
0
1
2
P
∴的分布列为
………………10分
∴
……………………12分
（
可以不扣分）
20．解：（1）依题意，
即
当
两式相减得，得
∴
……………………4分
当n=1时，
∴
=1适合上式……………………5分
故
…………………………6分
（2）由题意，
∴
………………10分
不等式
恒成立，即
恒成立.…………11分
经检验：
时均适合题意（写出一个即可）.……………………12分
21．解：（1）设
，
由条件知
∴
故C的方程为：
……………………4分
（2）由
∴
…………………………5分
设l与椭圆C交点为
（*）
……………………7分
∵
∴
∴
消去
∴
整理得
………………9分
，
因
，
∴
∴
∴
容易验证
所以（*）成立
即所求m的取值范围为
………………12分
22．（1）证明：假设存在
使得
∴
∵
…………………………2分
∴
∴
上的单调增函数.……………………5分
∴
是唯一的.……………………6分
（2）设
∵
∴
上的单调减函数.
∴
……………………8分
∵
∴
…………10分
∵
…………12分
∴
∴
为钝角
∴△ABC为钝角三角形.……………………14分
，
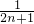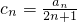，试判断并说明cn+1-cn（n∈N*）的符号；
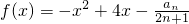，是否存在最大的实数λ，当x≤λ时，对于一切自然数n，都有f（x）≤0．
．
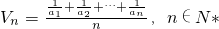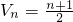，求数列{an}的通项公式an；
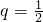，其倒数均为Vn，若存在正整数k，使n≥k时，Vn＜-16恒成立，试求k的最小值．