
题目列表(包括答案和解析)
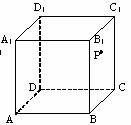 如图,在正方体
如图,在正方体![]() 中,P是侧面
中,P是侧面![]() 内一动点,若P到直线BC与直线
内一动点,若P到直线BC与直线![]() 的距离相等,则动点P的轨迹所在的曲线是
的距离相等,则动点P的轨迹所在的曲线是
(A)直线 (B)圆 (C)双曲线 (D) 抛物线
如图,在正方体![]() 中,P是侧面
中,P是侧面![]() 内一动点,若点P到直线BC的距离是点P到直线
内一动点,若点P到直线BC的距离是点P到直线![]() 距离的2倍,则动点P的轨迹所在的曲线是
距离的2倍,则动点P的轨迹所在的曲线是
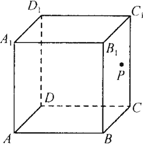
A.直线
B.椭圆
C.双曲线
D.抛物线
 6、如图,在正方体ABCD-A1B1C1D1中,P是侧面BB1C1C内一动点,若P到直线BC与直线C1D1的距离相等,则动点P的轨迹所在的曲线是( )
6、如图,在正方体ABCD-A1B1C1D1中,P是侧面BB1C1C内一动点,若P到直线BC与直线C1D1的距离相等,则动点P的轨迹所在的曲线是( )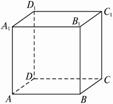
A.直线 B.圆 C.双曲线 D.抛物线
如图,在正方体ABCD—A1B1C1D1中,P是侧面BB1C1C内一动点,若点P到平面ABCD的距离等于它到直线C1D1的距离,则动点P的轨迹所在的曲线是
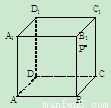
A.椭圆 B.双曲线
C.抛物线 D.圆
一、1―5 DCADC 6―10 DCBCD 11―12 CA
二、13.  14.
14.
 15.
140° 16.
15.
140° 16. 
三、17.解:


 ……………………… 8分
……………………… 8分
∵ ∴
∴
∴ ∴y的最小值为
∴y的最小值为 …………………… 10分
…………………… 10分
18.解:设
则:
∴ …………………………2分
…………………………2分
∴ ……………………………4分
……………………………4分
即:
∵ ∴
∴
∵ 且
且
∴
又
∴ …………………8分
…………………8分
 …………………10分
…………………10分
∴ …………………12分
…………………12分
19. (2分) 得
(2分) 得 将
将 或
或 (4分)
(4分)
当 即
即 时,
时, 在
在 上为增函数,不含题意(6分)
上为增函数,不含题意(6分)
当 即
即 时,
时, 在
在 上为增函数,在
上为增函数,在 内为减函数,在(
内为减函数,在( ) 上为增函数 (8分)
) 上为增函数 (8分)
∴当 时
时 ,当
,当 时
时 (10分)
(10分)
∴ 解得:
解得: (12分)
(12分)
 20.(1)略 (4分)
20.(1)略 (4分)
(2)解:过点C作 于M 连DM
于M 连DM
由(1)知: 面ABC ∴
面ABC ∴
∴ 是二面角D-AB-C的平面角(6分)
是二面角D-AB-C的平面角(6分)
设CD=1 ∵
∴ ∵
∵ 是正三角形
是正三角形
∴
∴
∴ (8分)
(8分)
 (3)取AB、AD、BC中点分别为M、N、O
(3)取AB、AD、BC中点分别为M、N、O
连AO、MO、NO、MN、OD
则
∴ 是AC与BD所成的角。(10分)
是AC与BD所成的角。(10分)
∵ 是正三角形且平面
是正三角形且平面 平面BCD
平面BCD
∴ 面BCD
面BCD  是
是 ∴
∴
又∵ 面ABC ∴
面ABC ∴ 
在 中,
中,


∴
∴直线AC和BD所成角为 (12分)
(12分)
21.解:设
(1)若PQ 轴时
轴时 
 且
且 ∴
∴ ∴
∴
 ∴
∴ (4分)
(4分)
(2)若PQ不垂直x轴时,设
代入 得:
得:

∵
∴
=
= (8分)
(8分)
∵ ∴
∴ ∴
∴
∴ (10分) ∴
(10分) ∴ 
∴ w.w.w.k.s.5 u.c.o.m
w.w.w.k.s.5 u.c.o.m
 综上:
综上: (12分)
(12分)
22.(1)取CD中点为K,连MK、NK
 ∴
∴
∴面MNK//面ADD
∴ MN//面ADD
(2)设F为AD中点,则PF 面ABCD
面ABCD
作 于H 则
于H 则 ∴
∴ 为平面角
为平面角
 ∴
∴
∴
故二面角P-AE-D的大小为 (8分)
(8分)
(3)
D到面 的距离为
的距离为
∴ (12分)
(12分)
www.ks5u.com
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com