
题目列表(包括答案和解析)
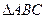 中,
中,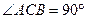 ,
,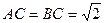 ,
,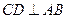 ,
,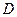 为垂足.沿
为垂足.沿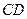 将
将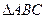 对折,连结
对折,连结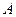 、
、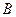 ,使得
,使得 .
.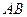 上是否存在点
上是否存在点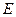 ,使
,使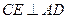 ?若存在,求出
?若存在,求出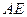 的长;若不存在,说明理由;
的长;若不存在,说明理由; 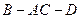 的平面角的正切值.
的平面角的正切值.
|
(本小题满分14分)
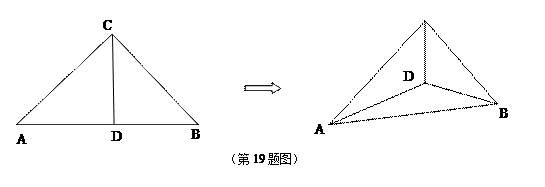
如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA,AC、CB、BP的中点.

(1)求证:D、E、F、G四点共面;
(2)求证:PC⊥AB;
(3)若△ABC和△PAB都是等腰直角三角形,且AB=2,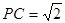 ,求四面体PABC的体积.
,求四面体PABC的体积.
(本小题满分14分)
如图,在直四棱柱ABCD-A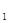 B
B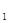 C
C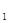 D
D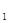 中,底面ABCD为等腰梯形,AB//CD,AB=4,
BC=CD=2,
中,底面ABCD为等腰梯形,AB//CD,AB=4,
BC=CD=2,
AA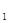 =2,
E、E
=2,
E、E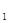 分别是棱AD、AA
分别是棱AD、AA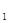 的中点.
的中点.
(1)设F是棱AB的中点,证明:直线EE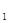 //平面FCC
//平面FCC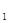 ;
;
(2)证明:平面D1AC⊥平面BB1C1C.

(本小题满分14分)如图,已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线 在y轴上的截距为m(m≠0),
在y轴上的截距为m(m≠0), 交椭圆于A、B两个不同点。
交椭圆于A、B两个不同点。
(1)求椭圆的方程;
(2)求m的取值范围;
(3)求证直线MA、MB与x轴始终围成一个等腰三角形。

(本小题满分14分)
如图,已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线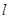 在y轴上的截距为m(m≠0),
在y轴上的截距为m(m≠0),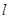 交椭圆于A、B两个不同点。
交椭圆于A、B两个不同点。
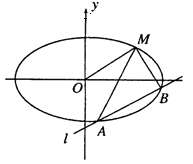
(1)求椭圆的方程;
(2)求m的取值范围;
(3)求证直线MA、MB与x轴始终围成一个等腰三角形。
一、选择题(本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
题号
1
2
3
4
5
6
7
8
9
10
答案
D
C
B
B
C
A
D
B
A
C
 二、填空题(每小题4分,共28分)
二、填空题(每小题4分,共28分)
11.1+2i
12.5
13.  14. 13
14. 13
15. 2或 16.
16.  17.9
17.9
三、解答题:本大题共5小题,满分72分.解答须写出文字说明、证明过程和演算步骤.
18.(本题满分14分)
解:(1)f(x)= T=4
T=4
(2) (3)
(3) 两边平方得
两边平方得
 ,而
,而 ∴
∴
 19.(本小题满分14分)
19.(本小题满分14分)
(1)证明:∵A/O⊥面CEFB
∴EF⊥A/O,又EF⊥EC
A/O∩EC=0
∴EF⊥面A/EC
而A/C 面A/EC
面A/EC
∴EF⊥A/C
(2)
20.(本题满分14分)
解:(1)an+1=2Sn+1,an=2Sn-1+1两式相减得an+1=3an(a≥2),又a2=2S1+1=
∴ {an}是以a1=1为首项,3为公比的等比数列,an=3n-1
{an}是以a1=1为首项,3为公比的等比数列,an=3n-1
(2)Tn= 5n2+20n
5n2+20n
21.(本小题满分15分)
解:(1)W:x2=6y
(2)设AC:
设A(x1,y1),C(x2,y2) |AC|=6(k2+1)
同理|BD|=6
SABCD=
当k=±1时取等号
22.(本小题满分15分)
解:(1)f(x)=ax3 4ax2+4ax
4ax2+4ax
f/(x)=3ax2 8ax+
8ax+ 2)(x
2)(x 2)=0
2)=0 x=
x= 或2
或2
∵f(x)有极大值32,而f(2)=0
∴f( )=32=7,a=27
)=32=7,a=27
(2)f/(x)=a(3x 2)(x
2)(x 2)
2)
当a>0时,f(x)=[  2,
2, ]上递增在[
]上递增在[ ]上递减,
]上递减,
 ∴0<a<
∴0<a<
当a<0时,f(x)在[ 2,
2, ]上递减,在[
]上递减,在[ ]上递增
]上递增
f( 2)=
2)= 
 ∴
∴
综上
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com