
题目列表(包括答案和解析)
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计. 请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:
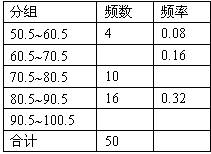
(Ⅰ)填充频率分布表的空格(将答案直接填在表格内);
(Ⅱ)补全频数条形图;
(Ⅲ)若成绩在75.5~85.5分的学生为二等奖,问获得二等奖的学生约为多少人?
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计. 请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
| 分组 | 频数 | 频率 | 频率/组距 |
| 50.5~60.5 | 4 | 0.08 | 0.008 |
| 60.5~70.5 | 0.16 | 0.016 | |
| 70.5~80.5 | 10 | ||
| 80.5~90.5 | 16 | 0.32 | 0.032 |
| 90.5~100.5 | |||
| 合计 | 50 |
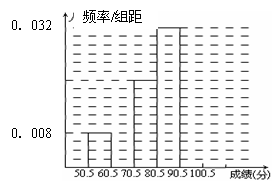
(1)填充频率分布表的空格(将答案直接填在表格内);
(2)补全频率分布直方图;
(3)若成绩在75.5~85.5分的学生为二等奖,问获得二等奖的学生约为多少人?
(14分)为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计. 请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:
| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 0.16 | |
| 70.5~80.5 | 10 | |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | ||
| 合计 | 50 |
(Ⅰ)填充频率分布表的空格(将答案直接填在表格内);
(Ⅱ)补全频数条形图;
(Ⅲ)若成绩在75.5~85.5分的学生为二等奖,问获得二等奖的学生约为多少人?
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计. 请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
| 分组 | 频数 | 频率 | 频率/组距 |
| 50.5~60.5 | 4 | 0.08 | 0.008 |
| 60.5~70.5 | 0.16 | 0.016 | |
| 70.5~80.5 | 10 | ||
| 80.5~90.5 | 16 | 0.32 | 0.032 |
| 90.5~100.5 | |||
| 合计 | 50 |
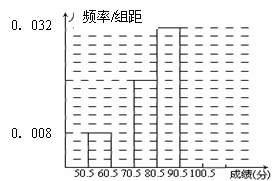
(1)填充频率分布表的空格(将答案直接填在表格内);
(2)补全频率分布直方图;
(3)若成绩在75.5~85.5分的学生为二等奖,问获得二等奖的学生约为多少人?
(14分)为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计. 请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:
| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 0.16 | |
| 70.5~80.5 | 10 | |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | ||
| 合计 | 50 |

(Ⅰ)填充频率分布表的空格(将答案直接填在表格内);
(Ⅱ)补全频数条形图;
(Ⅲ)若成绩在75.5~85.5分的学生为二等奖,问获得二等奖的学生约为多少人?
一、选择题(8小题,每题5分,共40分)
题号
1
2
3
4
5
6
7
8
9
10
答案
D
B
B
B
A
C
D
B
A
D
二、填空题(6小题,每题5分,共30分)
11. 5 ; 12. 13.15
13.15 ; 15 14。2; 15.
; 15 14。2; 15.
三、解答题(6小题,共80分)
16.解:(1)
 |
----------------5分
因为最小正周期为 ,∴
,∴ ,∴
,∴ ;----------6分
;----------6分
(2)由(1)知 ,
,
因为 ,∴
,∴ -------------------8分
-------------------8分
因为 ,∴
,∴
所以 或
或 ----------------10分
----------------10分
所以 或
或 .------------------12分
.------------------12分
17.解:(1)已知函数 ,
,  ------2分
------2分
又函数 图象在点
图象在点 处的切线与直线
处的切线与直线 平行,且函数
平行,且函数 在
在 处取得极值,
处取得极值, ,且
,且 ,解得
,解得
 ,且
,且 --------------5分
--------------5分
令

 ,
,
所以函数的单调递减区间为 -----------------8分
-----------------8分
(2)当 时,
时, ,又函数
,又函数 在
在 上是减函数
上是减函数
 在
在 上恒成立, --------------10分
上恒成立, --------------10分
即 在
在 上恒成立
上恒成立 。----------------12分
。----------------12分
 18.解:(1)
18.解:(1)
分组
频数
频率
50.5~60.5
4
0.08
60.5~70.5
8
0.16
70.5~80.5
10
0.20
80.5~90.5
16
0.32
90.5~100.5
12
0.24
合计
50
1.00
---------------------4分
(2) 频数直方图如右上所示--------------------------------8分
(3) 成绩在75.5~80.5分的学生占70.5~80.5分的学生的 ,因为成绩在70.5~80.5分的学生频率为0.2 ,所以成绩在76.5~80.5分的学生频率为0.1 ,---------10分
,因为成绩在70.5~80.5分的学生频率为0.2 ,所以成绩在76.5~80.5分的学生频率为0.1 ,---------10分
成绩在80.5~85.5分的学生占80.5~90.5分的学生的 ,因为成绩在80.5~90.5分的学生频率为0.32 ,所以成绩在80.5~85.5分的学生频率为0.16
-------------12分
,因为成绩在80.5~90.5分的学生频率为0.32 ,所以成绩在80.5~85.5分的学生频率为0.16
-------------12分
所以成绩在76.5~85.5分的学生频率为0.26,
由于有900名学生参加了这次竞赛,
所以该校获得二等奖的学生约为0.26´900=234(人) -------------14分
19.解(Ⅰ)证明:∵PA⊥底面ABCD,MN 底面ABCD
底面ABCD
∴MN⊥PA 又MN⊥AD 且PA∩AD=A
∴MN⊥平面PAD ………………3分
MN 平面PMN ∴平面PMN⊥平面PAD …………4分
平面PMN ∴平面PMN⊥平面PAD …………4分
(Ⅱ)∵BC⊥BA BC⊥PA PA∩BA=A ∴BC⊥平面PBA
∴∠BPC为直线PC与平面PBA所成的角
即 …………7分
…………7分
在Rt△PBC中,PC=BC/sin∠BPC=

∴ ………………10分
………………10分
(Ⅲ)由(Ⅰ)MN⊥平面PAD知 PM⊥MN MQ⊥MN
∴∠PMQ即为二面角P―MN―Q的平面角 …………12分
而 ∴
∴ …………14分
…………14分
20.(14分)
解(1) ,动圆的半径为r,则|PQ1|=r+3,
,动圆的半径为r,则|PQ1|=r+3,
|PQ2|= r+1,|PQ1|-|PQ2|=2,…………………3分
点P的轨迹是以O1、O2为焦点的双曲线右支,a=1,c=2,
方程为 ………………………………………………6分
………………………………………………6分
(2)设P(x1,y1),Q(x2,y2),当k不存在时,不合题意.
直线PQ的方程为y=k(x-3),
则

 ………………8分
………………8分
由
 、
、
 …………………………………………………………10分
…………………………………………………………10分
 …………14分
…………14分
21. (1)设 ----------------3
----------------3
 ,又
,又
 ---------------------------------5
---------------------------------5
(2)由已知得
两式相减得 ,
, -------------------------7
-------------------------7
当 .若
.若
 -------------------------------9分
-------------------------------9分
(3) 由 ,
,

 .-----------------------------------11分
.-----------------------------------11分
若
 ------------------------------13
------------------------------13
可知,
 -------------------------------14. 分
-------------------------------14. 分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com