题目列表(包括答案和解析)
（本小题满分12分）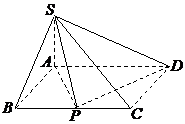
如图，四棱锥
的底面是矩形，
底面
，P为BC边的中点，SB与
平面ABCD所成的角为45°，且AD=2，SA=1．
（1）求证：
平面SAP；
（2）求二面角A－SD－P的大小.
（本小题满分12分）
如图，在四棱锥P－ABCD中，PB⊥底面
，CD⊥PD，底面ABCD为直角梯形，AD∥BC，AB⊥BC，AB=AD=PB=3，点E在棱PA上，且PE=2EA。（1）求异面直线PA与CD所成的角；（2）求证：PC∥平面EBD；（3）求二面角A－BE－D的大小。
（本小题满分12分）
如图，在四棱锥P－ABCD中，底面为正文形，PA
平面ABCD，且PA＝AD，E为棱PC上的一点，PD平面ABE
（I）求证：E为PC的中点
（II）若N为CD中点，M为AB上的动点，当直线MN与平面ABE所成的角最大时，求二面角C－EM—N的大小 
（本小题满分12分）如图，四棱锥P－ABCD的底面ABCD是直角梯形，∠DAB＝∠ABC＝90o，PA⊥底面ABCD，PA＝AB＝AD＝2，BC＝1，E为PD的中点．
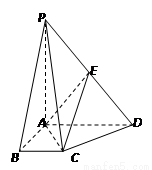
(1) 求证：CE∥平面PAB；
(2) 求PA与平面ACE所成角的大小；
(3) 求二面角E－AC－D的大小．
（本小题满分12分）
已知一四棱锥P－ABCD的三视图如下，E是侧棱PC上的动点。
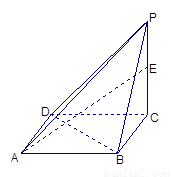
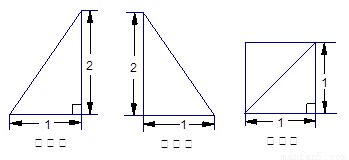
（Ⅰ）求四棱锥P－ABCD的体积；
（Ⅱ）当点E在何位置时，BD⊥AE？证明你的结论;
（Ⅲ）若点E为PC的中点，求二面角D－AE－B的大小．
一、选择题
1．B 2．A 3．C 4．B 5．B 6．D 7．C 8．C 9．D 10．A
二、填空题
11．
12．
13．－6 14．
；
15．①②③④
三、解答题
16．解：⑴
＝
＝
＝
＝
3分
＝
＝1＋1＋2cos2x＝2＋2cos2x＝4cos2x
∵x∈[0，
] ∴cosx≥0
∴
＝2cosx 6分
⑵ f (x)＝cos2x－
?2cosx?sinx＝cos2x－sin2x
＝2cos(2x＋
) 8分
∵0≤x≤ ∴
∴
∴
∴
，当x＝时取得该最小值
，当x＝0时取得该最大值 12分
17．由题意知，在甲盒中放一球概率为
时，在乙盒放一球的概率为
2分
①当n＝3时，x＝3，y＝0的概率为
4分
②当n＝4时，x＋y＝4，又|x－y|＝ξ，所以ξ的可能取值为0，2，4
(i)当ξ＝0时，有x＝2，y＝2，它的概率为
4分
(ii)当ξ＝2时，有x＝3，y＝1或x＝1，y＝3
它的概率为
(iii)当ξ＝4时，有x＝4，y＝0或x＝0，y＝4
它的概率为
故ξ的分布列为
ξ
0
2
4
10分
p
∴ξ的数学期望Eξ＝
12分
18．解：⑴证明：在正方形ABCD中，AB⊥BC
又∵PB⊥BC ∴BC⊥面PAB ∴BC⊥PA
同理CD⊥PA ∴PA⊥面ABCD 4分
⑵在AD上取一点O使AO=AD，连接E，O，
则EO∥PA，∴EO⊥面ABCD 过点O做
OH⊥AC交AC于H点，连接EH，则EH⊥AC，
从而∠EHO为二面角E－AC－D的平面角 6分
在△PAD中，EO＝AP＝
在△AHO中∠HAO＝45°，
∴HO＝AOsin45°=
，∴tan∠EHO＝
，
∴二面角E－AC－D等于arctan
8分
⑶当F为BC中点时，PF∥面EAC，理由如下：
∵AD∥2FC，∴
，又由已知有
，∴PF∥ES
∵PF
面EAC，EC
面EAC ∴PF∥面EAC，
即当F为BC中点时，PF∥面EAC 12分
19．⑴据题意，得
4分
5分
⑵由⑴得：当5＜x＜7时，y＝39(2x3－39x2＋252x－535)
当5＜x＜6时，y'＞0，y＝f (x)为增函数
当6＜x＜7时，y'＜0，y＝f (x)为减函数
∴当x＝6时，f (x)极大值＝f (16)＝195 8分
当7≤x＜8时，y＝6(33－x)∈(150，156]
当x≥8时，y＝－10(x－9)2＋160
当x＝9时，y极大＝160 10分
综上知：当x＝6时，总利润最大，最大值为195 12分
20．⑴设M(x0，y0)，则N(x0，－y0)，P(x，y)
|
②
4分
)
8分
的距离
总相切． 13分
，0) 2分
，得
，有
3分
4分
5分
，那么
7分
成立 9分
(可参照给分)
，
，∴
∵
∴
，综上
即证
11分
当x＞0时，f ' (x)＜0