练习册

  • 练习册
  • 试题
    2．答卷前将密封线内的各个项目正确填写清楚.同时在指定位置上填写两位数的座号. 【查看更多】

     

    题目列表(包括答案和解析)

    家用冰箱是一种常用的用电器，它是利用了叫做氟利昂的物质作为“热”的搬运工，把冰箱冷冻室的热搬运到冰箱外面，试问
        （1）氟利昂是一种具备什么特性的物质？电动压缩机是通过什么方式液化氟利昂的？
        （2）氟利昂对生态有一定的破坏作用，现在各国都在研制和生产氟利昂的代用品，氟利昂对环境有什么影响？
        （3）用一只标有3000r/kW?h的电能表来测定电冰箱的电功率，现在只让电冰箱单独工作3min，小明记下转盘转过的转数为30转，那么测得该电冰箱的实际功率是多大？
        （4）为了测定电冰箱每天消耗的电能，要求在测定前一小时内不开冰箱，冷冻食品也不要搬出，小明记下电冰箱某次开始工作的时刻3点20分，停机时刻3点30分，再记下接着下一次的开始工作时刻4点整，那么该冰箱每天工作耗电多少度？
        （5）想一想，电冰箱所处的环境的温度和开启冰箱门的次数对消耗的电功有什么影响？
        （6）用笔画线代替导线，将图中电冰箱的A接线柱正确连入三角插头中（其他接线不作要求），并说明为什么要这样连接？

    查看答案和解析>>

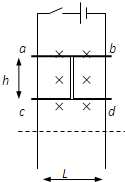    （2012?嘉定区一模）如图所示，宽为L的光滑长金属导轨固定在竖直平面内，不计电阻．将两根质量均为m的水平金属杆ab、cd用长h的绝缘轻杆连接在一起，放置在轨道上并与轨道接触良好，ab电阻R，cd电阻2R．虚线上方区域内存在水平方向的匀强磁场，磁感应强度B．
    （1）闭合电键，释放两杆后能保持静止，则ab杆受的磁场力多大？
    （2）断开电键，静止释放金属杆，当cd杆离开磁场的瞬间，ab杆上焦耳热功率为P，则此时两杆速度为多少？
    （3）断开电键，静止释放金属杆，若磁感应强度B随时间变化规律为B=kt（k为已知常数），求cd杆离开磁场前，两杆内的感应电流大小．某同学认为：上述情况中磁通量的变化规律与两金属杆静止不动时相同，可以采用△φ=△B?Lh 计算磁通量的改变量…该同学的想法是否正确？若正确，说明理由并求出结果；若不正确，说明理由并给出正确解答．

    查看答案和解析>>

    （2007?茂名一模）如图左所示，边长为l和L的矩形线框aa′、bb′互相垂直，彼此绝缘，可绕中心轴O1O2转动，将两线框的始端并在一起接到滑环C，末端并在一起接到滑环D，C、D彼此绝缘．通过电刷跟C、D连接．线框处于磁铁和圆柱形铁芯之间的磁场中，磁场边缘中心的张角为45°，如图右所示（图中的圆表示圆柱形铁芯，它使磁铁和铁芯之间的磁场沿半径方向，如图箭头所示）．不论线框转到磁场中的什么位置，磁场的方向总是沿着线框平面．磁场中长为l的线框边所在处的磁感应强度大小恒为B，设线框aa′和bb′的电阻都是r，两个线框以角速度ω逆时针匀速转动，电阻R=2r．
    （1）求线框aa′转到图右位置时感应电动势的大小；
    （2）求转动过程中电阻R上的电压最大值；
    （3）从线框aa′进入磁场开始，作出0～T（T是线框转动周期）时间内通过R的电流iR随时间变化的图象；
    （4）求外力驱动两线框转动一周所做的功．

    查看答案和解析>>

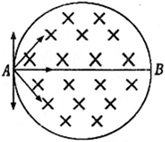    精英家教网如图所示，一匀强磁场磁感应强度为B，方向垂直纸面向里，其边界是半径为R的圆，AB为圆的一直径，在A点有一粒子源向圆平面内的各个方向发射质量m、电量-q的粒子，粒子重力不计．
    （1）有一带电粒子以v1=
    2qBRm
    的速度垂直磁场进入圆形区域，恰从B点射出．求此粒子在磁场中运动的时间．
    （2）若磁场的边界是绝缘弹性边界（粒子与边界碰撞后将以原速率反弹），某粒子沿半径方向射入磁场，经过2次碰撞后回到A点，则该粒子的速度为多大？

    查看答案和解析>>

    （2009?淄博二模）如图所示为一质点做匀变速直线运动的v-t图象，质点的质量为2kg，质点在前4s内向东运动，则根据图线作出的以下判断正确的是（　　）

    查看答案和解析>>

     

    一、选择题：本题共10个小题，每小题4分，共40分。在每个小题给出的四个选项中，至少有一个是正确的。每小题全选对的得4分；选对但不全的得2分；有选错或不答的得0分。

    1．C  2．AB  3．B  4．AD  5．C  6．BD

    7．B  8．ACD  9．BCD  10．D

     

    二、实验题：本题共2个小题，满分12分，把答案直接填在题中的横线上。

    11．（6分，每空2分，有效数字位数错误的每空扣1分）

        4.00  0.500  2.00 

    12．ACEFH（2分）；实物连接如图所示（滑动变阻器分压和限流接法都可以）（4分）

     

     

     

     

     

     

     

     

     

     

     

     

    三、计算题：本题共4小题，满分48分，解答应写出必要的文字说明、方程式和重要的演算步骤。只写出最后答案的不能得分。有数值计算的题，答案中必须明确写出数值和单位。

    13．（1）设小球到达d点处速度为v，由动能定理，得

              ①（2分）

           小球由d点做平抛运动，有   ②  （1分）

                 ③  （1分）

           联立①②③并代入数值，解得小球从最高点d抛出后的水平射程：

                  ④   （1分）

       （2）当小球通过d点是时，由ko jfy ,hko

    牛顿第二定律得

                  ⑤  （1分）

           代入数值解得管道对小球作用力N=1.1N，方向竖直向下。  ⑥（2分）

       （3）设小球到达c点处速度为vc，由动能定理，得

                ⑦  （2分）

           当小球通过c点时，由牛顿第二定律得ko点时

     

                  ⑧  （1分）

           要使轨道对地面的压力为零，则有

                  ⑨  （1分）

           联立①②③并代入数值，解得小球的最小速度：

              ⑩  （1分）

     

     

     

     

     

     

     

     

     

                 ①（1分）

                   ②  （1分）

                  ③   （1分）

           求出       ④  （1分）

           方向与x轴负方向成45°角  （1分）

           用其它方法求出正确答案的同样给分。

       （2）带电质点从P2到P3，重力与电场力平衡，洛伦兹力提供向心力

                  ⑤  （1分）

                 ⑥  （1分）

                   ⑦  （1分）

           由⑤解得：         ⑧  （1分）

           联立④⑥⑦式得   ⑨  （1分）

       （3）带电质点进入第四象限，水平方向做匀速直线运动，竖直方向做匀减速直线运动。当竖直方向的速度减小到0，此时质点速度最小，即v在水平方向的分量

              ⑩  （2分）

           方向沿x轴正方向（1分）

    15．解：（1）A、C两状态体积相等，则有

                ①

           得：   ②

       （2）由理想气体状态方程

                  ③

           得：   ④

           由此可知A|B两状态温度相同，故A、B两状态内能相等

           而该过程体积增大，气体对外做功，

           气体吸收热量       ⑤

           评分标准：本题共10分。其中①②③每式2分，④式1分，⑤式3分

    16．解：（1）由 图知：A=8┩

             ②

                ③

     

     

     

     

     

     

     

           评分标准：本题共10分，其中，①②③每式2分，正确作图4分。

     

     


    同步练习册答案