题目列表(包括答案和解析)
已知动圆C过点A(－2，0)，且与圆M：(x－2)2＋y2＝64相内切．
(1)求动圆C的圆心的轨迹方程；
(2)设直线l：y＝kx＋m(其中k，m∈Z)与(1)所求轨迹交于不同两点B，D，与双曲线
交于不同两点E，F，问是否存在直线l，使得向量
，若存在，指出这样的直线有多少条？若不存在，请说明理由．
已知动圆C过点A(－2，0)，且与圆M：(x－2)2＋y2＝64相内切．
(1)求动圆C的圆心的轨迹方程；
(2)设直线l：y＝kx＋m(其中k，m∈Z)与(1)所求轨迹交于不同两点B，D，与双曲线
交于不同两点E，F，问是否存在直线l，使得向量
，若存在，指出这样的直线有多少条？若不存在，请说明理由．
已知动圆C过点A(－2，0)，且与圆M：(x－2)2＋y2＝64相内切．
(1)求动圆C的圆心的轨迹方程；
(2)设直线l：y＝kx＋m(其中k，m∈Z与(1)中所求轨迹交于不同两点B，D，与双曲线
交于不同两点E，F，问是否存在直线l，使得向量
，若存在，指出这样的直线有多少条？若不存在，请说明理由．
（本小题16分）已知点A(-1, 0)、B(1, 0),△ABC的周长为2＋2.记动点C的轨迹
为曲线W.
(1)直接写出W的方程（不写过程）；
(2)经过点（0, ）且斜率为k的直线l与曲线W 有两个不同的交点P和Q，是否存在常数k，使得向量
与向量
共线？如果存在，求出k的值；如果不存在，请说明理由.
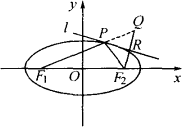
（3）设W的左右焦点分别为F1、 F2，点R在直线l：x－
y＋8＝0上．当∠F1RF2取最大值时，求
的值.
已知椭圆
＋
＝1(a＞b＞0)，点P为其上一点，F1，F2为椭圆的焦点，∠F1PF2的外角平分线为l，点F2关于l的对称点为Q，F2Q交l于点R．
(1)当P点在椭圆上运动时，求R形成的轨迹方程；
(2)设点R形成的曲线为C，直线l：y＝k(x＋
a)与曲线C相交于A，B两点，当△AOB的面积取得最大值时，求k的值．
一、选择题
1．D 2．A 3．C 4．D 5．B 6．C 7．D 8．B 9．A 10．A
二、填空题
11．148 12．－4 13．
14．－6 15．①②③④
三、解答题
16．解：⑴
＝
＝
＝
＝
3分
＝
＝1＋1＋2cos2x
＝2＋2cos2x
＝4cos2x
∵x∈[0，
] ∴cosx≥0
∴
＝2cosx 6分
⑵ f (x)＝cos2x－
?2cosx?sinx
＝cos2x－sin2x
＝2cos(2x＋
) 8分
∵0≤x≤ ∴
∴
∴
∴
，当x＝时取得该最小值
，当x＝0时取得该最大值 12分
17．由题意知，在甲盒中放一球概率为
，在乙盒放一球的概率为
3分
①当n＝3时，x＝3，y＝0的概率为
6分
②|x－y|＝2时，有x＝3，y＝1或x＝1，y＝3
它的概率为
12分
18．解：⑴证明：在正方形ABCD中，AB⊥BC
又∵PB⊥BC ∴BC⊥面PAB ∴BC⊥PA
同理CD⊥PA ∴PA⊥面ABCD 4分
⑵在AD上取一点O使AO=AD，连接E，O，
则EO∥PA，∴EO⊥面ABCD 过点O做
OH⊥AC交AC于H点，连接EH，则EH⊥AC，
从而∠EHO为二面角E－AC－D的平面角 6分
在△PAD中，EO＝AP＝
在△AHO中∠HAO＝45°，
∴HO＝AOsin45°=
，∴tan∠EHO＝
，
∴二面角E－AC－D等于arctan
8分
⑶当F为BC中点时，PF∥面EAC，理由如下：
∵AD∥2FC，∴
，又由已知有
，∴PF∥ES
∵PF
面EAC，EC
面EAC ∴PF∥面EAC，
即当F为BC中点时，PF∥面EAC 12分
19．⑴f '(x)＝3x2＋2bx＋c，由题知f '(1)＝0
3＋2b＋c＝0，
f (1)＝－11＋b＋c＋2＝－1
∴b＝1，c＝－5 3分
f (x)＝x3＋x2－5x＋2，f '(x)＝3x2＋2x－5
f (x)在[－
，1]为减函数，f (x)在(1，＋∞)为增函数
∴b＝1，c＝－5符合题意 5分
⑵即方程：
恰有三个不同的实解：
x3＋x2－5x＋2＝k(x≠0)
即当x≠0时，f (x)的图象与直线y＝k恰有三个不同的交点，
由⑴知f (x)在
为增函数，
f (x)在
为减函数，f (x)在(1，＋∞)为增函数，
又
，f (1)＝－1，f (2)＝2
∴
且k≠2 12分
20．⑴∵
∴
3分
∴{an－3n}是以首项为a1－3＝2，公比为－2的等比数列
∴an－3n＝2?(－2)n－1
∴an＝3n＋2?(－2)n－1＝3n－(－2)n 6分
⑵由3nbn＝n?(3n－an)＝n?[3n－3n＋(－2)n]＝n?(－2)n
∴bn＝n?(－)n 8分
令
∴
∴
∴
＜6
∴m≥6 13分
21．⑴设M(x0，y0)，则N(x0，－y0)，P(x，y)
AM：y＝
①
BN：y＝
②
联立①② ∴
4分
∵点M(xo，yo)在圆⊙O上，代入圆的方程：
整理：y2＝－2(x＋1) (x＜－1) 6分
⑵由
设S(x1、y1)，T(x2、y2)，ST的中点坐标(x0、y0)
则x1＋x2＝－(3＋
)
x1x2＝
8分
∴
中点到直线
的距离
∴
故圆与x＝－
总相切． 14分
⑵另解：∵y2＝－2(x＋1)知焦点坐标为(－
，0) 2分
顶点(－1，0)，故准线x＝－ 4分
设S、T到准线的距离为d1，d2，ST的中点O'，O'到x＝－的距离为
又由抛物线定义：d1＋d2＝|ST|，∴
故以ST为直径的圆与x＝－总相切 8分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com