
题目列表(包括答案和解析)
(本小题满分12分)
已知F1、F2分别是双曲线x2-y2=1的两个焦点,O为坐标原点,圆O是以F1F2为直径的圆,直线l:y=kx+b (b>0)与圆O相切,并与双曲线相交于A、B两点.
(1)根据条件求出b和k满足的关系式;
(2)向量 在向量
在向量 方向的投影是p,当(×)p2=1时,求直线l的方程;
方向的投影是p,当(×)p2=1时,求直线l的方程;
(3)当(×)p2=m且满足2≤m≤4时,求DAOB面积的取值范围.
(本小题满分12分)
已知F1、F2分别是双曲线x2-y2=1的两个焦点,O为坐标原点,圆O是以F1F2为直径的圆,直线l:y=kx+b (b>0)与圆O相切,并与双曲线相交于A、B两点.
(Ⅰ)根据条件求出b和k满足的关系式;
(Ⅱ)向量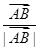 在向量
在向量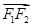 方向的投影是p,当(×)p2=1时,求直线l的方程;
方向的投影是p,当(×)p2=1时,求直线l的方程;
(Ⅲ)当(×)p2=m且满足2≤m≤4时,求DAOB面积的取值范围.
(本小题满分12分)
已知双曲线过点P ,它的渐近线方程为
,它的渐近线方程为
(1)求双曲线的标准方程;
(2)设F1和F2是这双曲线的左、右焦点,点P在这双曲线上,且|PF1|·|PF2|=32,求∠F1PF2的大小.
(本小题满分12分)
已知椭圆![]()
![]() 与双曲线
与双曲线![]() 有共同的焦点F1、F2,设它们在第一象限的交点为P,且
有共同的焦点F1、F2,设它们在第一象限的交点为P,且![]()
(1)求椭圆的方程;
(2)已知N(0,-1),对于(1)中的椭圆,是否存在斜率为![]() 的直线
的直线![]() ,与椭圆交于不同的两点A、B,点Q满足
,与椭圆交于不同的两点A、B,点Q满足![]() ?若存在,求出
?若存在,求出![]() 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
(本小题满分12分)
已知椭圆![]() 与双曲线
与双曲线![]() 有共同的焦点F1、F2,设它们在第一象限的交点为P,且
有共同的焦点F1、F2,设它们在第一象限的交点为P,且![]()
(1)求椭圆的方程;
(2)已知N(0,-1),对于(1)中的椭圆,是否存在斜率为![]() 的直线
的直线![]() ,与椭圆交于不同的两点A、B,点Q满足
,与椭圆交于不同的两点A、B,点Q满足![]() ?若存在,求出
?若存在,求出![]() 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
B
C
A
B
A
C
B
B
理D 文B
D
理D 文C
二.填空题
13.(理)-1;(文) (-1,1)∪(2,+∞). 14. 90.
15. .files/image208.gif) ;
16. (理)x+2y-3=0; (文)
;
16. (理)x+2y-3=0; (文).files/image210.gif) .
.
三.解答题
17. 解:(I).files/image212.gif) 平移以后得
平移以后得
.files/image214.gif) ,又
,又.files/image216.gif) 关于
关于.files/image160.gif) 对称
对称 .files/image219.gif)
.files/image221.gif)
.files/image223.gif) ,
, .files/image225.gif)
.files/image227.gif) ,
,
当且仅当.files/image229.gif) 时取最大值,
时取最大值,
所以,取得最大值时的集合为.files/image231.gif) .…………6分
.…………6分
(II).files/image162.gif) 的最小正周期为
的最小正周期为.files/image233.gif) ;
;.files/image235.gif) ,
,
.files/image237.gif) ,
,.files/image162.gif) 在[
在[.files/image165.gif) 上的值域为
上的值域为.files/image239.gif) .…………12分
.…………12分
18.解:(I)当n∈N.files/image241.gif) 时有:
时有:.files/image170.gif) =2
=2.files/image168.gif) -3n, ∴
-3n, ∴.files/image243.gif) =2
=2.files/image245.gif) -3(n+1),
-3(n+1),
两式相减得:.files/image245.gif) =2
=2.files/image245.gif) -2
-2.files/image168.gif) -3 ∴
-3 ∴.files/image245.gif) =2
=2.files/image168.gif) +3。 ……3分
+3。 ……3分
∴.files/image245.gif) +3=2(
+3=2(.files/image168.gif) +3)。
+3)。
又.files/image247.gif) =
=.files/image249.gif) =2
=2.files/image247.gif) -3, ∴
-3, ∴.files/image247.gif) =3,
=3, .files/image247.gif) +3=6≠0 ……4分
+3=6≠0 ……4分
∴数列{.files/image168.gif) +3}是首项6,公比为2的等比数列.从而c=3. ……6分
+3}是首项6,公比为2的等比数列.从而c=3. ……6分
(II)由(1)知:.files/image168.gif) +3=
+3=.files/image251.gif) , ∴
, ∴.files/image168.gif) =
=.files/image253.gif) -3. ………8分
-3. ………8分
(Ⅲ)假设数列{.files/image168.gif) }中是否存在三项
}中是否存在三项.files/image255.gif) ,
,.files/image257.gif) ,
,.files/image259.gif) ,(r<s<t),它们可以构成等差数列,
,(r<s<t),它们可以构成等差数列,
∵.files/image255.gif) <
<.files/image257.gif) <
<.files/image259.gif) , ∴只能是
, ∴只能是.files/image255.gif) +
+.files/image259.gif) =2
=2.files/image257.gif) ,
,
∴(.files/image261.gif) -3)+(
-3)+(.files/image263.gif) -3)=2(
-3)=2(.files/image265.gif) -3)
-3)
即.files/image267.gif) +
+.files/image269.gif) =
=.files/image271.gif) .∴1+
.∴1+.files/image273.gif) =
=.files/image275.gif) .
. .files/image277.gif)
∵r<s<t,r、s、t均为正整数,∴.files/image277.gif) 式左边为奇数右边为偶数,不可能成立.
式左边为奇数右边为偶数,不可能成立.
因此数列{.files/image168.gif) }中不存在可以构成等差数列的三项. ………12分
}中不存在可以构成等差数列的三项. ………12分
19. (理)解:设从甲袋中取出.files/image279.gif) 个白球的事件为
个白球的事件为.files/image281.gif) ,从乙袋中取出
,从乙袋中取出.files/image279.gif) 个白球的事件为
个白球的事件为.files/image283.gif) 其中
其中.files/image279.gif) =0,1,2,则
=0,1,2,则.files/image285.gif) ,
,.files/image287.gif) .
.
(I).files/image289.gif) ,
,.files/image291.gif) ,
,
所以.files/image293.gif) ………………………..6分
………………………..6分
(II).files/image174.gif) 分布列是
分布列是
.files/image174.gif)
0
1
2
3
4
P
.files/image296.gif)
.files/image298.gif)
.files/image300.gif)
.files/image302.gif)
.files/image304.gif)
.files/image306.gif) ……………12分
……………12分
(文) 19.(I)三人恰好买到同一只股票的概率.files/image308.gif) 。 ……4分
。 ……4分
(II)解法一:三人中恰好有两个买到同一只股票的概率.files/image310.gif) .……9分
.……9分
由(I)知,三人恰好买到同一只股票的概率为.files/image312.gif) ,所以三人中至少有两人买到同一只股票的概率
,所以三人中至少有两人买到同一只股票的概率.files/image314.gif) 。 ……12分
。 ……12分
|