题目列表(包括答案和解析)
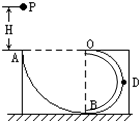如图所示，ABDO是处于竖直平面内的固定光滑轨道，AB是半径为R=15m的| 1 | 4 |
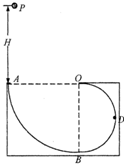如图所示，ABDO是处于竖直平面内的光滑轨道，AB是半径为R=15m的| 1 | 4 |
（13分）如图所示，ABDO是处于竖直平面内的固定光滑轨道，AB是半径为R=15m的
圆周轨道，半径OA处于水平位置，BDO是半径为 r =7.5m的半圆轨道，D为BDO轨道的中点。一个小球P从A点的正上方距水平半径OA高H处自由下落，沿竖直平面内的轨道通过D点时对轨道的压力等于重力的
倍。g取10m/s2。求：
（1）H的大小。
（2）试讨论此球能否达到BDO轨道的O点，并说明理由。
（3）小球沿轨道运动后再次落到轨道上的速度大小是多少？
（12分）如图所示，ABDO是处于竖直平面内的光滑轨道，AB是半径为R=15m的
圆周轨道，半径OA处于水平位置，BDO是直径为d=15m的半圆轨道，D为BDO轨道的中央，一个小球P从A点的正上方距水平半径OA高H处自由落下，沿竖直平面内的轨道通过D点时对轨道的压力等于其重力的
倍，取g为10m/s2。
（1）H的大小；
（2）试讨论此球能否到达BDO轨道的O点，并说明理由；
（3）小球沿轨道运动后再次落到轨道上的速度的大小是多少。
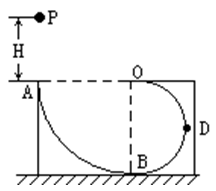
（20分）如图所示，ABDO是处于竖直平面内的光滑轨道，AB是半径为R=15m的1/4圆周轨道，半径OA处于水平位置，BDO是直径为15m的半圆轨道，D为BDO轨道的中央.一个小球P从A点的正上方距水平半径OA高H处自由落下，沿竖直平面内的轨道通过D点时对轨道的压力等于其重力的14/3倍.取g为10m/s2.
（1）H的大小；
（2）试讨论此球能否到达BDO轨道的O点，并说明理由；
（3）小球沿轨道运动后再次落到轨道上的速度的大小是多少.
。
1．答案：A 由滚轮不会打滑可知主动轴上的平盘与可随从动轴转动的圆柱形滚轮的接触
点的线速度相同，所以v1=v2，由此可得
，所以
，即选项A
正确.
2．答案：B 根据物体作直线运动和曲线运动的条件可知，先作初速度为零的沿合力方向的匀加速直线运动，后因速度方向跟另一个力不在一条直线上，作匀变速曲线运动.
3．答案：AC
根据运动的合成与分解，因为小船垂直岸航行，渡河时间与水的速度无关，又河水的流速与到河岸的距离x成正比，即
，所以
，解得
，渡河时间为
.
4．答案：C 小球做平抛运动，竖直高度
m，A正确；小球水平方向上的位移
m，小球初速度
m/s，此即第一次闪光时小车的速度，B正确；两次闪光时间间隔内汽车的平均速度
m/s，因此汽车应做加速运动，C不能确定，D能够确定.
5．答案：CD 根据物体竖直上抛的运动规律，得
，因此可求出该星球表面的重力加速度g.再根据
可推导出CD为正确答案.
6．答案：A 因为要提高“神舟”六号飞船的高度将考虑启动火箭发动机向后喷气，通过反冲作用，使飞船加速，飞船需要的向心力增大，但由于在原轨道上
不变，不足以提供其所需的向心力，所以飞船做离心运动，到更高的轨道，所以A正确，B错误.对飞船有：
，所以
，R增大，运行速度v减小，C错误；由于
，所以
，
，所以R增大，T增大，但a减少，所以D错.
7．答案：C 在理想情况下一直加速，可以达到围绕地球表面做圆周运动，即第一宇宙速度.
8．答案：C 球的水平速度是
，解得
m/s.
9．答案：C 设杆沿方向移动的速度为
，根据速度分解可得，
，
，所以可得
.
10．答案：BC 
较小，物体追上细杆相碰；较大，细杆绕过一周后追上物体相碰.
第Ⅱ卷（非选择题，共110分）
11．（1）答案：平抛运动在竖直方向上是自由落体运动 （2分）
球1落到光滑水平板上并击中球2（2分）
平抛运动在水平方向上是匀速运动（2分）
（2）答案：如图所示，测量R、r、R/，（2分）
自行车的速度为：
.（2分）
12．解析：（1）根据游标卡尺的读数原理，可得读数应为主尺上的和游标尺上的刻度相加.由图乙可知游标尺的分度为
（2）由题意知，纸带上每两点的时间间隔T=0.10s，打下计数点D时，纸带运动速度大小为：
cm/s2=
此时圆盘转动的角速度为
=6.5rad/s
（3）纸带运动的加速度大小为
，代入数值，得a=
设角加速度为β，则
=9.8rad/s2.
13．解析：对物体受力分析可知正压力
①，其中
表示气动压力. （3分）
②，（4分）
根据牛顿第二定律，可得
③，（3分）
联立解得，
（2分）
14．解析：第一个等式（对热气球）不正确，因为热气球不同于人造卫星，热气球静止在空中是因为浮力与重力平衡，它绕地心运动的角速度应等于地球自转的角速度. （4分）
（1）若补充地球表面的重力加速度为g，可以认为热气球受到的万有引力近似等于其重力，则有
（2分）
与第二个等式联立可得
（1分）
（2）若利用同步卫星的离地高度H有：
（2分）
与第二个等式联立可得
（2分）
（3）若利用第一宇宙速度v1，有
（2分）
与第二个等式联立可得
（1分）
此外若利用近地卫星运行的角速度也可求出来.
15．解析：水滴沿切线方向做平抛运动到地面上的水平位移
=
落地时间
s（2分）
“魔盘”的线速度
m/s（2分）
其转速满足
（2分）
r/min. （2分）
16．解析：（1）卫星做匀速圆周运动，由万有引力和牛顿第二定律得，
（2分）
其动能为
（2分）
其机械能为E=Ek+Ep=
+(
)=
（4分）
卫星绕地表运行时，r=R，且
，GM=gR2，（2分）
所以E=
=
=－6.4×106×10×103=－3.2×1010J. （4分）
（2）要使绕地球运动的卫星挣脱地球的引力，需添加的能量是：
ㄓE=0－E=3.2×1010J. （4分）
17．解析：（1）小球从H高处自由落下，进入轨道，沿BDO轨道做圆周运动，小球受重力和轨道的支持力.设小球通过D点的速度为v，通过D点时轨道对小球的支持力为F（大小等于小球对轨道的压力）提供它做圆周运动的向心力，即
①（2分）
小球从P点落下一直到沿光滑轨道运动的过程中，机械能守恒有，
②（2分）
由①②解得高度
m（1分）
（2）设小球能够沿竖直轨道运动到O点时的最小速度为v0，则有
③（2分）
小球至少应从H0高处落下，
④（1分）
由③④可得
（1分）
由H>H0，小球可以通过O点. （1分）
（3）小球由H落下通过O点的速度为
m/s（1分）
小球通过O点后做平抛运动，设小球经过时间t落到AB圆弧轨道上，
建立图示的坐标系，有
⑤（1分）
⑥（1分） 且
⑦（1分）
由⑤⑥⑦可解得时间t=1s（负解舍去）（1分）
落到轨道上速度大小为
m/s（1分）
18．解析：（1）当飞船以v0绕月球做半径为rA=R+h的
圆周运动时，由牛顿第二定律得，
（2分）
则
（2分）
式中M表示月球的质量，R为月球的半径，
为月球表面的重力加速度，
所以代入数据得，v0=
（2）根据开普勒第二定律，飞船在A、B两处的面积速度相等，所以有rAvA=rBvB，
即(R+h)vA=RvB ①（2分）
由机械能守恒定律得，
②（2分）
由①②式并代入数据得，vA=
故登月所需速度的改变量为
m/s（2分）
飞船在A点喷气前后动量守恒，设喷气总质量为ㄓm，因喷气前的动量为mv0，喷气后的动量为(m－ㄓm)vA+ㄓm(v0+u)，前后动量相等，
故有mv0=(m－ㄓm)vA+ㄓm(v0+u)，（2 分）
故喷气所消耗的燃料的质量为ㄓm=mㄓv/(u+ㄓv)=
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com