题目列表(包括答案和解析)
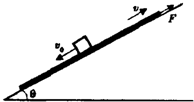如图所示，在倾角为θ=37°的足够长的斜面上，有质量为m1=2kg的长木板．开始时，长木板上有一质量为m2=1kg的小铁块（视为质点）以相对地面的初速度v0=2m/s 从长木板的中点沿长木板向下滑动，同时长木板在沿斜面向上的拉力作用下始终做速度为v=1m/s的匀速运动，小铁块最终与长木板一起沿斜面向上做匀速运动．已知小铁块与长木板、长木板与斜面间的动摩擦因数均为μ=0.9，重力加速度为g=10m/s2，sin37°=0.6，cos37°=0.8
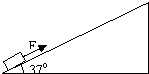如图所示，在倾角为θ=37°的足够长的固定足够长的斜面底端有一质量为m=2kg的物体，物体与斜面间动摩擦因数为μ=0.25．现用轻细绳将物体由静止沿斜面向上拉动，拉力F=20N，方向平行斜面向上．经时间t1=4s绳子突然断裂，求：（sin37°=0.6，cos37°=0.8，g=10m/s2）
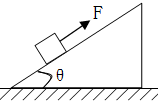如图所示，在倾角为θ=37°的足够长的固定斜面上有一质量m=1kg的物体，物体与斜面间的动摩擦因素μ=0.2．物体受到沿平行于斜面向上的轻细线的拉力F=9.6N的作用．从静止开始运动．经2s绳子突然断了．如图所示，在倾角为θ=37°的足够长的光滑斜面上，质量都为M=2 kg的长方体板A和B之间夹有少许炸药，在B的左端叠放有一质量为m=1 kg的物体C(视为质点)，C与B之间的动摩擦因数μ=0.75．现无初速同时释放它们，当它们沿斜面滑行s=3 m时，炸药瞬间爆炸，爆炸完毕时A的速度为vA=12 m/s．此后，C始终未从B的上表面滑落．问：B的长度至少多大？（取g=10m/s2．爆炸不会影响各物体的质量和各表面的光滑程度．）
如图所示，在倾角为θ=37°的足够长的固定斜面上，物体A和小车B正沿着斜面上滑，A的质量为mA=0．50kg，B的质量为mB=0．25kg，A始终受到沿斜面向上的恒力F的作用．当A追上B时，A的速度为vA=1．8m/s，方向沿斜面向上，B的速度恰好为零，A、B相碰，相互作用时间极短，相互作用力很大，碰撞后的瞬间，A的速度变为v1=0．6m/s，方向沿斜面向上．再经T=0．6s，A的速度大小变为v2=1．8m/s，在这一段时间内A、B没有再次相碰．已知A与斜面间的动摩擦因数μ=0．15，B与斜面间的摩擦力不计，已知：sin37°=0．6，重力加速度g=10m/s2，求：
（1）A、B第一次碰撞后B的速度；方向沿斜面向上
（2）恒力F的大小．
1．答案：A 根据核反应方程中质量数和电荷数守恒可得．
2．答案：A 由
衰变规律，质量数不变，质子数增加1，
比
质子增加2，所以发生2次衰变．
3．答案：B 由动能定理知功相同，结合前动能相同，
，因此
，碰撞过程动量守恒，
，故碰后速度v一定与PA相同，向右．
4．答案：C 根据爱因斯坦的质能方程知
，
，
，
=92．16MeV．
5．答案：B小球与墙壁碰撞后，如果无能量损失，则小球应以相同的速率返回，这种情况动量变化量
最大等于2mv，动能变化量
最小为零，所以②正确；如果小球与墙壁碰后粘在墙上，动量变化量最小等于mv，动能变化量最大等于
，所以④正确．
6．答案：D 由
可知X粒子为
．
7．答案：D 利用放射线消除有害静电是利用
射线的电离性，使空气分子电离成倒替，将静电泄出；
射线对人体细胞伤害太大，因此不能用来人体透视，在用于治疗肿瘤时要严格控制剂量；DNA变异并不一定都是有益的，也有时发生变害的一面．
8．答案：A 
，
，
，
根据
，可得
，则
．
9．答案：D 由动量守恒定律pA=pA/+pB，再由德布罗意波长公式λ=h/p，得到
h/λ1=h/λ2+h/λ3．
10．答案：D 平台光滑，说明小孩和木板组成的系统动量守恒．小孩从木板右端B向左端A走动时，木板将沿平台向右移动，二者相对于平台的动量的大小相等，即
。设经过时间
小孩走到A端，则
，即
，又
m。联立二式解得，
m．此时，木板的重心已向右移到了平台上，即使小孩从左端A离开木板，木板也不会翻倒，故D正确．
11．答案：（1）根据题意得，
O
N+
e，e+
e2
．（2分）
（2）B正确． （2分）
（3）根据E=h=mc2和c=
/υ可得=h/mc． （2分）
（4）根据同位素的用途，半衰期应极短． （2分）
12．答案：（1）接通打点计时器的电源 （2分） 放开滑块1 （2分） （2）0．620 （2分） 0．618 （2分） （3）纸带与打点计时器限位孔有摩擦（4分）
解析：作用前系统的总动量为滑块1的动量p0=m1v0．
v0=0．2/0．1=
块2的动量和，且此时两滑块具有相同的速度v，v=0．168/0．14=1．
p=(m1+m2)v=(0．310+0．205)×1．2=0．
13．解析：水从h高处落下可认为是自由落体运动，速度为v，则
（2分）
m/s①（2分）
设在很短时间t内有质量为m的水落到石头上，以它为研究对象，设石头对水的平均作
用力为F，取竖直向下为正方向，由动量定理得，
②，而
③
（5分）
由①②③式代入数据解得，
N（2分）
根据牛顿第三定律可知，水对石头的反作用力
=N． （2分）
14．解析：设X衰变时放出的α粒子的速度为
，在磁场中做匀速圆周运动的半径为r，则由上图可知，
（1分）又
=
，（1分）
所以
．（2分）
因衰变过程中动量守恒，故有
，（2分）
．（2分）
衰变过程中释放的能量为
（2分）
由爱因斯坦质能方程，得
（2分）
故原子核X的质量为
．（2分）
15．解析：（1）可发射6种频率的光子（4分）
（2）由玻尔的跃迁规律可得光子的能量为
，代入数据得E=2．55eV（3分）
（3）E只大于铯的逸出功，故光子只有照射铯金属上时才能发生光电效应．
根据爱因斯坦的光电效应方程可得光电子的最大初动能为
（3分）
代入数据得，
eV（或1．0×10－19J）（3分）
16．解析：（1）A、B碰撞过程中满足动量守恒，mAvA=mAv1+mBvB（2分）
得vB=2．
方向沿斜面向上（1分）
（2）设经过时间T=0．60s，A的速度方向向上，此时A的位移
m（1
分）
B的加速度aB=gsinθ=
B的位移
m（1分）
可见A、B将再次相碰，违反了题意，因此碰撞后A先做匀减速运动，速度减为零后，
再做匀加速运动．（1分）
对A列出牛顿第二定律：mAgsinθ+μmgcosθ－F=mAa1，（2分）
mAgsinθ－μmgcosθ－F=mAa2，（2分）
v1=a1t1，v2=a2(T－t1) （2分）
解得F=0．6N（1分）
17．解析：解：以彗星和撞击器组成的系统为研究对象，设彗星的质量为M，初速度为v01，撞击器质量m=
由动量守恒定律得：
① （4分）
由于M远大于m，所以，上式可以化为：
②（4分）
解得： 
③（2分）
由题给信息知，撞击后彗星的运行速度改变了0．
m/s ④ （3分）
代入③式解得 M≈4×
18．解析：（1）小球由静止摆到最低点的过程中，有
（2分）
（1分）
小球与物块Q相撞时，没有能量损失，动量守恒，机械能守恒，
，（1分）
，（1分）
解得，
，
（1分）
二者交换速度，即小球静止下来，而（1分）
Q在平板车上滑行的过程中，有
（1分）
（1分）
小物块Q离开平板车时，速度为
（1分）
（2）由能的转化和守恒定律，知
（1分）
（1分）
解得，
（1分）
（3）小物块Q在平板车上滑行过程中，对地位移为s，则
（1分）
解得，
（1分）
平抛时间
（1分）
水平距离
（1分）
Q落地点距小球的水平距离为
（1分）
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com