题目列表(包括答案和解析)
如图所示，空间存在着强度E=2.5×102N/C方向竖直向上的匀强电场，在电场内一长为L=0.5m的绝缘细线，一端固定在O点，一端拴着质量m=0.5kg、电荷量q=4×10-2C的小球．现将细线拉直到水平位置，使小球由静止释放，当小球运动最高点时细线受到的拉力恰好达到它能承受的最大值而断裂．取g=10m/s2．求：如图所示，空间存在着强度E=2.5×102N/C方向竖直向上的匀强电场，在电场内一长为L=0.5m的绝缘细线，一端固定在O点，一端拴着质量m=0.5kg、电荷量q=4×10-2C的小球．现将细线拉直到水平位置，使小球由静止释放，当小球运动最高点时细线受到的拉力恰好达到它能承受的最大值而断裂．取g=10m/s2．求：如图所示，空间存在着强度E=2.5×102N/C方向竖直向上的匀强电场，在电场内一长为L=0.5m的绝缘细线，一端固定在O点，一端拴着质量m=0.5kg、电荷量q=4×10－2C的小球.现将细线拉直到水平位置，使小球由静止释放，当小球运动最高点时细线受到的拉力恰好达到它能承受的最大值而断裂.取g=10m/s2.求：
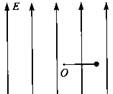
（1）小球的电性；
（2）细线能承受的最大拉力；
（3）当小球继续运动后与O点水平方向距离为L时，小球距O点的高度.
如图所示，空间存在着强度E=2.5×102N/C方向竖直向上的匀强电场，在电场内一长为L=0.5m的绝缘细线，一端固定在O点，一端拴着质量m=0.5kg、电荷量q=4×10－2C的小球.现将细线拉直到水平位置，使小球由静止释放，当小球运动最高点时细线受到的拉力恰好达到它能承受的最大值而断裂.取g=10m/s2.求：
（1）小球的电性；
（2）细线能承受的最大拉力；
（3）当小球继续运动后与O点水平方向距离为L时，小球距O点的高度.
 |
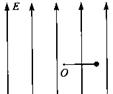（13分）如图所示，空间存在着强度E=2.5×102N/C方向竖直向上的匀强电场，在电场内一长为L=0.5m的绝缘细线，一端固定在O点，一端拴着质量m=0.5kg、电荷量q=4×10－2C的小球.现将细线拉直到水平位置，使小球由静止释放，当小球运动最高点时细线受到的拉力恰好达到它能承受的最大值而断裂.取g=10m/s2.
求：
（1）小球的电性；
（2）细线能承受的最大拉力；
（3）当小球继续运动后与O点水平方向距离为L时，小球距O点的高度.
1．答案：B 根据电场线疏密判断E的大小，密的地方场强大，有EA>EB；根据沿电场线方向电势降低，有
>
.
2．答案：A 由点电荷的电场分布特点可知，距离点电荷越近，场强越大，因此该点电荷必然处于A点右侧.但点电荷带电性质不确定，因此场强的方向不确定.
3．答案：BD 由电场的叠加，AB中垂线中由C向上场强为先增后减，故电荷C所受电场力向上且先增后减，所以C的加速度先增后减，但速度始终增大，可知BD正确.
4．答案：C 静电屏蔽作用，人体相当于一个等势体.
5．答案：BC 注意两种情况的区别，电键K始终闭合，则电容器两板间的电压保持不变，闭合后再断开则电量保持不变，然后再根据平行板电容器电容、电势差和电量的关系及匀强电场中场强和距离的关系即可.
6．答案：B 由于库仑力变化，因此质子向b不是做加速运动，A错误；由于a、b之间的电势差恒定，根据动能定理得，
可得
，则知
粒子从a点由静止释放后运动到b点的速率为
，B正确；当电子以Oa为半径绕O做匀速圆周运动时，根据
，可得
，则知电子以Ob为半径绕O做匀速圆周运动时的线速度为
，C、D错误.
7．答案：AD 减小的动能转化为电子的电势能，由A到C减小的动能与由C到B增加的动能相等，所以场强方向由O指向C，A和B的电势相等，形成电场的正电荷应位于D点.
8．答案：A 根据带电粒子在电场中水平方向上匀速和竖直方向上匀加速即可推出A正确.
9．答案：D 剪断细线Oc后，a、b作为一个系统在水平方向只受内力（库仑力、绳子拉伸后的拉力）作用，外力无冲量故其水平方向上动量恒为零.在竖直方向上，二者同时在重力作用下做初速度为零的匀加速运动，同时落地机械能守恒，故落地时，ab两球的动能和为
.在运动过程中，电场力做正功，因此其系统电势能减小.
10．答案：BD 粒子在水平方向上做匀速直线运动，因初速度相同，故水平位移
大的时间长，因
，故
，A错.粒子在竖直方向上做匀加速直线运动，有
，因为位移
相同，所以运动时间长的粒子加速度小，即
，故B正确.粒子到达正极板的动能为
，而
，所以有
，C错误.由可以判断A带负电，B不带电，C带正电，D正确.
11．答案：（1）BE（4分） 要用直流电源形成稳恒电流场，以模拟静电场，应选6V的直流电源，所以选B；要用探针寻找等势点，电流表灵敏度高，指针能左右偏转，所以选E.
（2）D （4分） 探针由O点左侧沿x轴正方向移到O点右侧的过程中，两探针间的电势差先减小后变大，所以灵敏电流表的指针与零刻度的夹角先变小后变大.
12．答案：（1）如图（a）.（4分）（2）
（4分）（3）
（4分）
提示：带电小球的受力如图b，
根据平衡条件有
，
又有
，联立解得，
，所以应以为横坐标.
13．解析：（1）由图可得B点电场强度的大小
N/C．（2分）
因B点的试探电荷带负电，而受力指向x轴的正方向，故B点场强的方向沿x轴的负方向. （2分）
（2）因A点的正电荷受力和B点的负电荷受力均指向x轴的正方向，
故点电荷Q位于A、B两点之间，带负电. （2分）
设点电荷Q的坐标为x，则
，
（4分）
由图可得
N/C，解得x=
14．解析：他的解答是错误的. （5分）
小环是穿在丝线上，作用于小环上的两个拉力大小相等，方向不同.小环受四个力，如图所示.
竖直方向 Tsin60°=mg
① （3分）
水平方向 Tcos60°+T=
② （3分）
由①②联立得 
（3分）
15．解析：（1）由小球运动到最高点可知，小球带正电（2分）
（2）设小球运动到最高点时速度为v，对该过程由动能定理有，
①（2分）
在最高点对小球由牛顿第二定律得，
②（2分）
由①②式解得，T=15N（1分）
（3）小球在细线断裂后，在竖直方向的加速度设为a，则
③（2分）
设小球在水平方向运动L的过程中，历时t，则
④（1分）
设竖直方向上的位移为s，则
⑤（1分）
由①③④⑤解得，s=
∴小球距O点高度为s+L=
16．解析：（1）因油滴到达最高点时速度大小为
，方向水平，对O→N过程用动能定理有
，（2分）
所以电场力一定做正功，油滴带负电，则最高位置一定在O点的左上方. （3分）
（2）由（1）的分析可知
，在竖直方向上油滴做初速为
的竖直上抛运动，则有
，（3分）
即
.（2分）
（3）油滴由O→N的运动时间
，（2分）
则在水平方向上由动量定理得，
（2分）
即
.（2分）
17．解析：（1）小球由B点运动到C点过程，由动能定理有，
，（2分）
在C点，设绳中张力为FC，则有
（2分）
因FC=mg，故vC=0（2分）
又由小球能平衡于A点得，
（2分）
（2分）
（2）小球由D点静止释放后将沿与竖直方向夹θ=53°的方向作匀加速直线运动，直至运动到O点正下方的P点，OP距离h=Lcot53°=
（2分）
在此过程中，绳中张力始终为零，故此过程的加速度a和位移s分别为：
，
.（2分）
∴小球到达悬点正下方时的速率为
.（2分）
18．解析：（1）设电子经电压U1加速后的速度为v0，根据动能定理得：
e U1=
………（2分） 解得：
………（2分）
（2）电子以速度v0进入偏转电场后，垂直于电场方向作匀速直线运动，沿电场方向作初速度为零的匀加速直线运动。设偏转电场的电场强度为E，电子在偏转电场运动的时间为t1，电子的加速度为a，离开偏转电场时相对于原运动方向的侧移量为y1，根据牛顿第二定律和运动学公式得：
F=eE， E=
， F=ma， a =
……（3分）
t1=
， y1=
，解得： y1=
……（3分）
（3）设电子离开偏转电场时沿电场方向的速度为vy，根据运动学公式得：vy=at1=
（2分）
电子离开偏转电场后作匀速直线运动，设电子离开偏转电场后打在荧光屏上所用的时间为t2，电子打到荧光屏上的侧移量为y2，如图所示
t2=
， y2= vyt2 解得：y2=
……………………（2分）
P到O点的距离为 y=y1+y2=
……………………（2分）
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com