练习册

  • 练习册
  • 试题
    20．如图所示.空间某平面内有一条折线是磁场的分界线.在折线的两侧分布着方向相反.与平面垂直的匀强磁场.磁感应强度大小都为B．折线的顶角∠A＝90°.P.Q是折线上的两点.AP=AQ=L．现有一质量为m.电荷量为q的带负电微粒从P点沿PQ方向射出.不计微粒的重力．(1)若P.Q间外加一与磁场方向垂直的匀强电场.能使速度为v0射出的微粒沿PQ直线运动到Q点.则场强为多大?(2)撤去电场.为使微粒从P点射出后.途经折线的顶点A而到达Q点.求初速度v应满足什么条件?中微粒从P点到达Q点所用时间的最小值． 【查看更多】

     

    题目列表(包括答案和解析)

    如图所示，空间某平面内有一条折线是磁场的分界线，在折线的两侧分布着方向相反、与平面垂直的匀强磁场，磁感应强度大小都为B．折线的顶角∠A=90°，P、Q是折线上的两点，AP=AQ=L．现有一质量为m、电荷量为q的带负电微粒从P点沿PQ方向射出，不计微粒的重力．
    （1）若P、Q间外加一与磁场方向垂直的匀强电场，能使速度为v0射出的微粒沿PQ直线运动到Q点，求其电场强度．
    （2）撤去电场，为使微粒从P点射出后，途经折线的顶点A而到达Q点，求初速度v应满足什么条件？
    （3）求第（2）中微粒从P点到达Q点所用时间的最小值．

    查看答案和解析>>

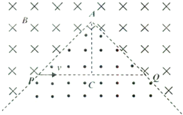    精英家教网如图所示，空间某平面内有一条折线是磁场的分界线，在折线PAQ的两侧分布着方向相反、与平面垂直的匀强磁场，磁感应强度大小都为B．折线的顶角∠A=90°，P、Q是折线上的两点，AP=AQ=
    		2
    L，C是线段PQ的中点．现有一质量为m、电荷量为q的带负电微粒从P点沿PQ方向射出，不计微粒的重力．
    （1）如果微粒恰好从顶点A第一次射出磁场分界线，则微粒的速度v1为多少；
    （2）如果微粒从P点射出后，途经折线的顶点A而到达Q点，剐微粒从P点到达Q点所经过的路程s为多少；
    （3）如果在以C为圆心、1.3L为半径的圆外没有磁场，为使微粒从P点射出后，途经折线的顶点A而到达Q点，且微粒经过A点时的速度不与PQ平行，则离子的最大速度vm为多少．

    查看答案和解析>>

    如图所示，空间某平面内有一条折线是磁场的分界线，在折线的两侧分布着方向相反、与平面垂直的匀强磁场，磁感应强度大小都为B。折线的顶角∠A＝90°，P、Q是折线上的两点， AP=AQ=L。现有一质量为m、电荷量为q的带负电微粒从P点沿PQ方向射出，不计微粒的重力。

    求：（1）若P、Q间外加一与磁场方向垂直的匀强电场，能使速度为v0射出的微粒沿PQ直线运动到Q点，则场强为多大？

    （2）撤去电场，为使微粒从P点射出后，途经折线的顶点A而到达Q点，求初速度v应满足什么条件？

    （3）求第（2）中微粒从P点到达Q点所用的时间。

              

    查看答案和解析>>

    如图所示，空间某平面内有一条折线是磁场的分界线，在折线的两侧分布着方向相反、与平面垂直的匀强磁场，磁感应强度大小都为B．折线的顶角∠A＝90°，P、Q是折线上的两点，AP=AQ=L．现有一质量为m、电荷量为q的带负电微粒从P点沿PQ方向射出，不计微粒的重力．

    （1）若P、Q间外加一与磁场方向垂直的匀强电场，能使速度为v0射出的微粒沿PQ直线运动到Q点，则场强为多大？方向如何？

    （2）撤去电场，为使微粒从P点射出后，途经折线的顶点A而到达Q点，求初速度v应满足什么条件？

    （3）求第（2）中微粒从P点到达Q点所用时间的最小值．

    查看答案和解析>>

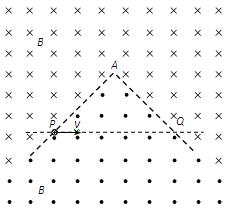
    如图所示，空间某平面内有一条折线是磁场的分界线，在折线的两侧分布着方向相反、与平面垂直的匀强磁场，磁感应强度大小都为B．折线的顶角∠A=90°，P、Q是折线上的两点，AP=AQ=L．现有一质量为m、电荷量为q的带负电微粒从P点沿PQ方向射出，不计微粒的重力．

    1.若在P、Q间外加一与磁场方向垂直的匀强电场，能使速度为射出的微粒沿PQ直线运动到Q点，则匀强电场的场强为多大?

    2.撤去(1)中的匀强电场，为使微粒从P点射出后，途经折线的顶点A而到达Q点，求初速度应满足什么条件?

    3.求第(2)问中微粒从P点到达Q点所用时间的最小值．

     

    查看答案和解析>>

    1. A 　2. BD 　 3.AD  4. B 　5.A  6.C　7.AC    8. BCD   9.A   10.AB   11.ACD    12.D

     

    13．（10分）

    （1）热力学第二定律（3分）

    （2）永不停息地做无规则运动（3分）   ；      （4分）

    14．（10分）

    （1）粒子性    （3分）

       （2）向下（3分）；   10m/s（4分）

     

    15．实验二：   

    （1）B、D、F、G、J、M   （3分）

      （2）①将实验装置按要求安装好

           ②接通电源，释放处于竖直状态的纸带。用刻度尺测量出纸带上相邻两点间的距离分别为d1、d2。

           ③计算重力加速度的表达式为   （3分）

        实验三：

      （1）G、L、M   （3分）

      （2）①将带光控计时器的平板用支架竖直架稳

        　　　 ②测量两个光控门之间的距离s

       　　　　③把滑块从上面的一个光控门处自由释放，读出下落时间t

    ④计算重力加速度的表达式为          （3分）

    评分说明：如有其他方法，只要实验原理正确，参照以上给分；实验步骤必须完整才给分。

     

    16．14分）（1） 52.75 （2分）

    （2）思路分析与参考答案：①A．电路如图所示，测电阻时应尽量使指针指在中间值附近，所以应选“×1k”．（2分）

       B．欧姆表中值电阻为R中 = 30×1kΩ= 30000Ω，欧姆表指n刻度，则电压表内电阻RV = 1000n，流过电压表电流IV = U/RV = U/(1000n)，根据闭合电路欧姆定律电池电动势E = U + IVR中 = U。（3分）

    ②　A．如图所示（3分）．

    ，所以不能用电流表；又电压表的量程较小于电源电动势，所以滑动变阻器应用分压接法．

    B．Ug = （2分），

    其中N：V表指针所指格数，U1：V1表读数．（2分）

     

    17．（共14分）

    解：（1）取最长的反应时间0.6s，最小的动摩擦因数0.32  　　　 …（4分）

    （2）根据牛顿第二定律，汽车刹车时的加速度

          ……（3分）

    考虑最高车速v、最长反应时间t、及最小动摩擦因数μ的极限情况下

    反应距离                ……（2分）

    制动距离          ……（3分）

    刹车距离               ……（2分）

    因此200m的安全距离是必要的。

     

    18．（16分）

    （1）如图所示，对质点受力分析可得：

    ……………………3’

    绳中的拉力T=mg/cosθ=750N………3’

    根据几何关系可得：……1‘

    代入数据得：rad/s………2’

        （2）转盘从静止启动到转速稳定这一过程，绳子对质点做的功等于质点机械能的增加量：………………………………………………4’

    m，m/s

    代入数据解得W=3450J………………………………………3’

     

    19． 解：⑴a球从O到M 

    WOM＝  （3分）

    得：     （2分）　  方向向左  （1分）

    ⑵设碰撞中损失的机械能为△E，对a、b球从O到N的全过程应用能的转化和守恒定律：

    　　　－qE2L－△E＝0－     （3分）

    则碰撞中损失的机械能为    △E＝= （3分） 

    ⑶设a与b碰撞前后的速度分别为v、v′，则 ：

    mv＝2mv’    （2分）    

    又减少的动能△E＝－＝  （2）

              （2分）

    20．（18分）

    解：（1）电场力与洛伦兹力平衡得：qE=qv0B得：E=v0B            （3分）

    （2）根据运动的对称性，微粒能从P点到达Q点，应满足   （2分）

    其中x为每次偏转圆弧对应的弦长，偏转圆弧对应的圆心角为或．

    设圆弧的半径为R，则有2R2=x2，可得：              （2分）

    又 由①②③式得：，n=1、2、3、……    （3分）

    （3）当n取奇数时，微粒从P到Q过程中圆心角的总和为

    ，（2分），其中n=1、3、5、……（1分）

    当n取偶数时，微粒从P到Q过程中圆心角的总和为：

    ，（2分），其中n=2、4、6、……（1分）

    欲使时间最小，取n=1或者2，此时 （2分）

     

     

     

     

     

     


    同步练习册答案