
题目列表(包括答案和解析)
在 中,
中,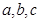 ,分别是角
,分别是角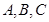 所对边的长,
所对边的长,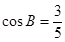 ,且
,且
(1)求 的面积;
的面积;
(2)若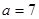 ,求角C.
,求角C.
【解析】第一问中,由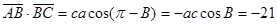 又∵
又∵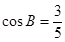 ∴
∴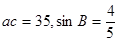 ∴
∴ 的面积为
的面积为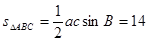
第二问中,∵a =7 ∴c=5由余弦定理得: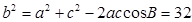 得到b的值,然后又由余弦定理得:
得到b的值,然后又由余弦定理得: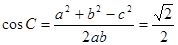
又C为内角 ∴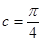
解:(1)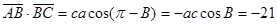 ………………2分
………………2分
又∵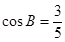 ∴
∴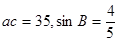 ……………………4分
……………………4分
∴ 的面积为
的面积为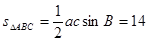 ……………………6分
……………………6分
(2)∵a =7 ∴c=5 ……………………7分
由余弦定理得: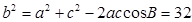
∴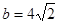 ……………………9分
……………………9分
又由余弦定理得: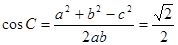
又C为内角 ∴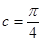 ……………………12分
……………………12分
另解:由正弦定理得: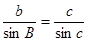 ∴
∴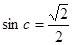 又
又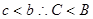 ∴
∴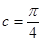
已知在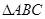 中,
中,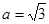 ,
,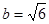 ,
,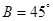 ,解这个三角形;
,解这个三角形;
【解析】本试题主要考查了正弦定理的运用。由正弦定理得到: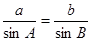
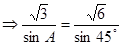 ,然后又
,然后又 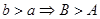
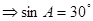
又 再又
再又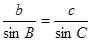 得到c。
得到c。
解:由正弦定理得到: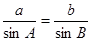
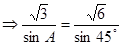
又 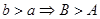
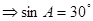 ……4分
……4分
又 ……8分
……8分
又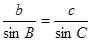
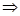
(本题满分18分,第(1)小题4分,第(2)小题6分,第(3)小题8分)
在平行四边形 中,已知过点
中,已知过点 的直线与线段
的直线与线段 分别相交于点
分别相交于点 。若
。若 。
。
(1)求证: 与
与 的关系为
的关系为 ;
;
(2)设 ,定义函数
,定义函数 ,点列
,点列 在函数
在函数 的图像上,且数列
的图像上,且数列 是以首项为1,公比为
是以首项为1,公比为 的等比数列,
的等比数列, 为原点,令
为原点,令 ,是否存在点
,是否存在点
 ,使得
,使得 ?若存在,请求出
?若存在,请求出 点坐标;若不存在,请说明理由。
点坐标;若不存在,请说明理由。
(3)设函数 为
为 上偶函数,当
上偶函数,当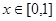 时
时 ,又函数
,又函数 图象关于直线
图象关于直线 对称, 当方程
对称, 当方程 在
在 上有两个不同的实数解时,求实数
上有两个不同的实数解时,求实数 的取值范围。
的取值范围。
已知正项数列 的前n项和
的前n项和 满足:
满足: ,
,
(1)求数列 的通项
的通项 和前n项和
和前n项和 ;
;
(2)求数列 的前n项和
的前n项和 ;
;
(3)证明:不等式  对任意的
对任意的 ,
, 都成立.
都成立.
【解析】第一问中,由于 所以
所以
两式作差 ,然后得到
,然后得到
从而 得到结论
得到结论
第二问中, 利用裂项求和的思想得到结论。
利用裂项求和的思想得到结论。
第三问中,

又
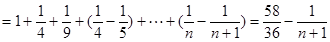
结合放缩法得到。
解:(1)∵ ∴
∴
∴
∴ ∴
∴  ………2分
………2分
又∵正项数列 ,∴
,∴ ∴
∴
又n=1时,
∴ ∴数列
∴数列 是以1为首项,2为公差的等差数列……………3分
是以1为首项,2为公差的等差数列……………3分
∴ …………………4分
…………………4分
∴ …………………5分
…………………5分
(2) …………………6分
…………………6分
∴
 …………………9分
…………………9分
(3)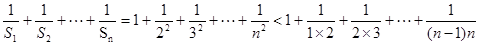
 …………………12分
…………………12分
又

 ,
,
∴不等式  对任意的
对任意的 ,
, 都成立.
都成立.
如图,已知⊙ 中,直径
中,直径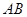 垂直于弦
垂直于弦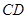 ,垂足为
,垂足为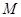 ,
,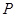 是
是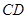 延长线上一点,
延长线上一点,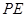 切⊙
切⊙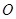 于点
于点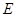 ,连接
,连接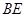 交
交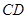 于点
于点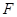 ,证明:
,证明: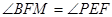
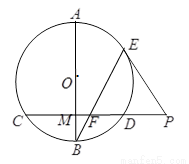
【解析】本试题主要考查了直线与圆的位置关系的运用。要证明角相等,一般运用相似三角形来得到,或者借助于弦切角定理等等。根据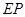 为⊙
为⊙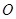 的切线,∴
的切线,∴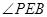 为弦切角
为弦切角
连接 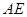 ∴
∴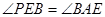 …注意到
…注意到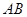 是直径且垂直弦
是直径且垂直弦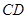 ,所以
,所以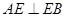 且
且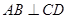 …利用
…利用 ,可以证明。
,可以证明。
解:∵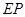 为⊙
为⊙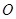 的切线,∴
的切线,∴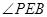 为弦切角
为弦切角
连接 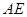 ∴
∴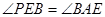 ……………………4分
……………………4分
又∵ 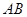 是直径且垂直弦
是直径且垂直弦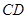 ∴
∴ 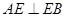 且
且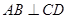 ……………………8分
……………………8分
∴  ∴
∴ 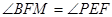
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com