题目列表(包括答案和解析)
(1)当k=0时,若g(x)=
的定义域为R,求实数m的取值范围;
(2)给出定理:若函数f(x)在［a,b］上连续,且f(a)·f(b)＜0,则函数y=f(x)在区间(a,b)内有零点,即存在x0∈(a,b),使f(x0)=0.运用此定理,试判断当k＞1时,函数f(x)在［k,2k］内是否存在零点.
(文)已知数列{an}的前n项和为Sn,a1=2,且nan+1=Sn+n(n+1)(n∈N*).
(1)求an;
(2)设bn=
,求{bn}的最大项.
已知二次函数
为偶函数，函数f（x）的图象与直线y=x相切．
（1）求f（x）的解析式
（2）已知k的取值范围为
,则是否存在区间[m，n]（m＜n
，使得f（x）在区间[m，n]上的值域恰好为[km，kn]？若存在，请求出区间[m，n]；若不存在，请说明理由．
已知二次函数f(x)=ax2+bx,f(x+1)为偶函数,函数f(x)的图象与直线y=x相切.
（I）求f(x)的解析式;
（II）已知k的取值范围为[
,+∞),则是否存在区间[m,n](m<n),使得f(x)在区间[m,n]上的值域恰好为[km,kn]?若存在,请求出区间[m,n];若不存在,请说明理由.
已知二次函数f(x)=ax2+bx,f(x+1)为偶函数,函数f(x)的图象与直线y=x相切.
（I）求f(x)的解析式;
（II）已知k的取值范围为[
,+∞),则是否存在区间[m,n](m<n),使得f(x)在区间[m,n]上的值域恰好为[km,kn]?若存在,请求出区间[m,n];若不存在,请说明理由.
已知二次函数f(x)=ax2+bx,f(x+1)为偶函数,函数f(x)的图象与直线y=x相切.
（I）求f(x)的解析式;
（II）已知k的取值范围为[
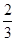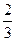,+∞),则是否存在区间[m, n](m<n),使得f(x)在区间[m,n]上的值域恰好为[km,kn]?若存在,请求出区间[m,n];若不存在,请说明理由.
一、填空题
1．
2．
3．既不充分条件又不必要条件 4．[－4，－π]
[0，π]
5．
6．6 7．
8．2个 9．等腰直角三角形
10．
11．（-3，4），（-1，2）
12．①、②、⑤
13．
14．C
二、解答题
15．（本小题满分14分）
解：（1）设
由
得
它的解集为（1，3）得方程
的两根为1和3且a<0
即
……（1）
……3分
有等根得
……（2）
……6分
由(1)(2)及
得
故
的解析式为
……8分
（2）由
及
……10分
由
……12分
解得 
……14分
16．（本小题满分14分）
解：由
得
，
………………………………2分
又
， ……………………………………6分
由
得
, …………………………10分
．
……14分
17．（本小题满分15分）．
已知二次函数的二次项系数为
，且不等式的解集为
．
（1）若方程
有两个相等的根，求的解析式；
（2）若的最大值为正数，求的取值范围．
解：（1）设由得
它的解集为（1，3）得方程的两根为1和3且a<0
即 ……（1）
……3分
有等根得
……（2）
……6分
由(1)(2)及得
故的解析式为
……8分
（2）由
及
……10分
由
……12分
解得 ……15分
18解：（1）当m＝2时，A＝（-2，2），B＝（-1，3）∴ A
B＝（-1，2）．……5分
（2）当m＜0时，B＝（1+m，1-m）
要使B
A，必须
，此时
m
当m＝0时，B＝
，BA；适合
……10分
当m＞0时，B＝（1-m，m＋1）
要使BA，必须
，此时0<m≤1． ……13分
∴综上可知，使BA的实数m的取值范围为[-1，1] ……15分
法2
要使BA，必须
，此时m1； ……13分
∴使BA的实数m的取值范围为[-1，1] ……15分
18．（本小题满分15分）
（1）解：由
得
，
． ………………2分
设
=
＜0(讨论a＞1和0＜a＜1)，
得f(x)为R上的增函数． ………………5分
（2）由
， …………7分
即
得
， ………………9分
得1＜m＜
.
………………10分
（3）f(x)在R上为增函数)f(x) 当
时)f(x)-4的值恒为负数， ………13分
而f(x)在R上单调递增得f(2)-40，
………………15分
19．（本小题满分16分）
解：（1）∵f（x+1）为偶函数，
∴
恒成立，
即（
∴
．
∵函数f（x）的图象与直线y=x相切，
∴二次方程
有两相等实数根，
∴
………………6分
（2）
………………8分
即
为方程
的两根
．
………………11分
∵m＜n且
．
故当
；
当k＞1时，
当k=1时，[m，n]不存在． ………………16分
20．（本小题满分16分）
解：（1）若
为函数f(x)不动点，则有
，
整理得 
①
………………2分
根据题意可判断方程①有两个根，且这两个根互为相反数，得
>
，
<0
所以b=3 ,a>0 ………………4分
而
，所以
．
即b=3，a>0，且a≠9. ………………5分
（2）在（1）的条件下，当a=8时，
．
由
，解得两个不动点为
，……6分
设点P(x ,y),则y>3 ,即
>3解得x<-3 ．
………………8分
设点P(x，y)到直线A
．
………………10分
当且仅当
，即x=―4时，取等号，此时P(―4，4)． ……12分
（3）命题正确． ………………13分
因为f(x)定义在R上的奇函数，所以f(―0)=―f(0) ,所以0是奇函数f(x)的一个不动点．
设c≠0是奇函数f(x)的一个不动点,则f(c)=c
,由
，所以―c也是f (x)的一个不动点．
所以奇函数f(x)的非零不动点如果存在,则必成对出现，故奇函数f(x)的不动点数目是奇数个． ………………16分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com