
题目列表(包括答案和解析)
已知x=-1是![]() 的一个极值点
的一个极值点
(1)求![]() 的值;
的值;
(2)求函数![]() 的单调增区间;
的单调增区间;
(3)设![]() ,试问过点(2,5)可作多少条直线与曲线y=g(x)相切?请说明理由。
,试问过点(2,5)可作多少条直线与曲线y=g(x)相切?请说明理由。
已知下列四个命题:
①若函数y=f(x)在x0处的导数![]() (x0)=0,则它在x=x0处有极值;
(x0)=0,则它在x=x0处有极值;
②若不论m为何值,直线y=mx+1均与曲线![]() 有公共点,则b≥1;
有公共点,则b≥1;
③若x、y、z∈R+,a=x+![]() ,b=y+
,b=y+![]() ,c=z+
,c=z+![]() ,则a、b、c中至少有一个不小于2;
,则a、b、c中至少有一个不小于2;
④若命题“存在x∈R,使得|x-a|+|x+1|≤2”是假命题,则|a+1|>2;
以上四个命题正确的是________(填入相应序号).
已知函数f(x)=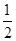 m(x-1)2-2x+3+ln x,m≥1.
m(x-1)2-2x+3+ln x,m≥1.
(1)当m= 时,求函数f(x)在区间[1,3]上的极小值;
时,求函数f(x)在区间[1,3]上的极小值;
(2)求证:函数f(x)存在单调递减区间[a,b];
(3)是否存在实数m,使曲线C:y=f(x)在点P(1,1)处的切线l与曲线C有且只有一个公共点?若存在,求出实数m的值;若不存在,请说明理由.
 m(x-1)2-2x+3+ln x,m≥1.
m(x-1)2-2x+3+ln x,m≥1. 时,求函数f(x)在区间[1,3]上的极小值;
时,求函数f(x)在区间[1,3]上的极小值;已知函数f(x)= m(x-1)2-2x+3+ln x,m≥1.
m(x-1)2-2x+3+ln x,m≥1.
(1)当m= 时,求函数f(x)在区间[1,3]上的极小值;
时,求函数f(x)在区间[1,3]上的极小值;
(2)求证:函数f(x)存在单调递减区间[a,b];
(3)是否存在实数m,使曲线C:y=f(x)在点P(1,1)处的切线l与曲线C有且只有一个公共点?若存在,求出实数m的值;若不存在,请说明理由.
一、填空题
⒈.files/image128.gif) ⒉
⒉.files/image130.gif) ⒊-i ⒋
⒊-i ⒋.files/image132.gif) ⒌
⒌.files/image134.gif)
⒍.files/image136.gif) ⒎
⒎.files/image138.gif) ⒏
⒏.files/image140.gif) ⒐
⒐.files/image142.gif) ⒑
⒑.files/image144.gif)
⒒14
⒓.files/image146.gif) ⒔
⒔.files/image148.gif) ⒕m>
⒕m>.files/image150.gif)
二、解答题
⒖解:(Ⅰ) .files/image076.gif)
.files/image152.gif)
.files/image154.gif)
.files/image156.gif) ……(4分)
……(4分)
∵函数.files/image158.gif) 的单调增区间为
的单调增区间为.files/image160.gif) ,
,.files/image162.gif)
∴.files/image164.gif) ,∴
,∴.files/image166.gif) ,
,.files/image162.gif)
∴函数f(x)的单调递增区间为.files/image168.gif) ,
,.files/image162.gif) ……(8分)
……(8分)
(Ⅱ)当.files/image078.gif) 时,
时,.files/image170.gif) ,∴
,∴.files/image172.gif)
∴函数f(x)的值域为.files/image174.gif) ……(14分)
……(14分)
⒗解:(Ⅰ) ∵DC⊥平面ABC,EB⊥平面ABC
∴DC//EB,又∵DC.files/image176.gif) 平面ABE,EB
平面ABE,EB.files/image178.gif) 平面ABE,∴DC∥平面ABE……(4分)
平面ABE,∴DC∥平面ABE……(4分)
(Ⅱ)∵DC⊥平面ABC,∴DC⊥AF,又∵AF⊥BC,∴AF⊥平面BCDE……(8分)
(Ⅲ)由(2)知AF⊥平面BCDE,∴AF⊥EF,在三角形DEF中,由计算知DF⊥EF,
∴EF⊥平面AFD,又EF.files/image178.gif) 平面AFE,∴平面AFD⊥平面AFE.……(14分)
平面AFE,∴平面AFD⊥平面AFE.……(14分)
⒘解:根据题意得,BC=.files/image086.gif) km,BD=
km,BD=
设∠ACD=α,∠CDB=β
在△CDB中,由余弦定理得
.files/image180.gif) ,所以
,所以.files/image182.gif)
于是.files/image184.gif) ……(7分)
……(7分)
在△ACD中,由正弦定理得
.files/image186.gif)
答:此人还得走.files/image188.gif) km到达A城……(14分)
km到达A城……(14分)
⒙解:(1) 因x=-1是.files/image088.gif) 的一个极值点
的一个极值点
∴ .files/image190.gif)
即 2+b-1=0
∴b= -1经检验,适合题意,所以b= -1.……(5分)
(2) .files/image192.gif)
∴.files/image192.gif) >0
>0
∴ .files/image194.gif) >0
>0
∴x>.files/image196.gif)
∴函数 的单调增区间为.files/image198.gif) ……(10分)
……(10分)
(3).files/image093.gif) =2x+lnx
=2x+lnx
设过点(2,5)与曲线g (x)的切线的切点坐标为.files/image201.gif)
∴.files/image203.gif)
即.files/image205.gif) ∴
∴.files/image207.gif)
令h(x)=.files/image209.gif)
∴.files/image211.gif) =
=.files/image213.gif) =0
=0
∴.files/image215.gif)
∴h(x)在(0,2)上单调递减,在(2,.files/image217.gif) )上单调递增
)上单调递增
.files/image219.gif) 又
又.files/image221.gif) ,h(2)=ln2-1<0,
,h(2)=ln2-1<0,.files/image223.gif)
∴h(x)与x轴有两个交点
∴过点(2,5)可作2条曲线y=g(x)的切线. ……(16分)
⒚解:(Ⅰ)∵.files/image099.gif) 为偶函数,∴
为偶函数,∴.files/image225.gif) ,∴
,∴.files/image227.gif) ,∴
,∴.files/image229.gif)
∴.files/image231.gif) ,∴函数
,∴函数.files/image101.gif) 为奇函数;……(4分)
为奇函数;……(4分)
(Ⅱ)⑴由.files/image234.gif) 得方程
得方程.files/image236.gif) 有不等实根
有不等实根
∴△.files/image238.gif) 及
及.files/image240.gif) 得
得.files/image242.gif) 即
即.files/image244.gif)
又.files/image099.gif) 的对称轴
的对称轴.files/image246.gif)
故.files/image099.gif) 在(-1,1)上是单调函数……………………………………………(10分)
在(-1,1)上是单调函数……………………………………………(10分)
⑵.files/image248.gif) 是方程(*)的根,∴
是方程(*)的根,∴.files/image250.gif)
∴.files/image252.gif) ,同理
,同理.files/image254.gif)
∴.files/image256.gif)
.files/image258.gif)
.files/image260.gif)
同理.files/image262.gif)
.files/image264.gif)
要使.files/image111.gif) ,只需
,只需.files/image266.gif) 即
即.files/image268.gif) ,∴
,∴.files/image270.gif)
或.files/image272.gif) 即
即.files/image274.gif) ,解集为
,解集为.files/image276.gif)
故.files/image043.gif) 的取值范围
的取值范围.files/image270.gif) ……(16分)
……(16分)
⒛(Ⅰ)证明:.files/image279.gif) ,
,.files/image281.gif)
由条件可得.files/image283.gif) ,所以
,所以.files/image285.gif) ……(4分)
……(4分)
(Ⅱ)解:因为bn+1=(-1)n+1[an+1-3(n-1)+9]=(-1)n+1(.files/image287.gif) an-2n+6)
an-2n+6)
=.files/image287.gif) (-1)n?(an-3n+9)=-
(-1)n?(an-3n+9)=-.files/image287.gif) bn
bn
又b1=.files/image289.gif) ,所以
,所以
当λ=-6时,bn=0(n∈N+),此时{bn}不是等比数列,
当λ≠-6时,b1=.files/image289.gif) ≠0,由上可知bn≠0,∴
≠0,由上可知bn≠0,∴.files/image292.gif) (n∈N+).
(n∈N+).
故当λ≠-6时,数列{bn}是以-(λ+6)为首项,-.files/image287.gif) 为公比的等比数列. ……(10分)
为公比的等比数列. ……(10分)
(Ⅲ)由(Ⅱ)知,当λ=-6,bn=0,Sn=0,不满足题目要求.
.files/image294.jpg)
当n为正奇数时,1<f(n).files/image296.gif)
∴f(n)的最大值为f(1)=.files/image298.gif) ,f(n)的最小值为f(2)=
,f(n)的最小值为f(2)= .files/image300.gif) ,
,
于是,由①式得.files/image302.gif) a<-
a<-.files/image304.gif) (λ+6)<
(λ+6)<.files/image306.gif)
当a<b.files/image308.gif)
.files/image310.gif) -
-
当b>
且λ的取值范围是(-b-6, -
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com