
题目列表(包括答案和解析)
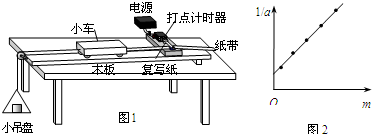
| 1 |
| k |
| 1 |
| k |
| b |
| k |
| b |
| k |

| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| SⅡ-SⅠ |
| 2(△t)2 |
| SⅡ-SⅠ |
| 2(△t)2 |
| 1 |
| k |
| 1 |
| k |
| b |
| k |
| b |
| k |
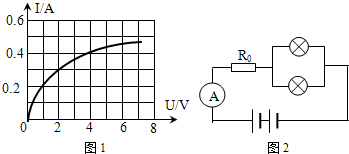 图1所示为一个灯泡两端的电压与通过它的电流的变化关系曲线,可见两者不呈线性关系,这是由于焦耳热使灯丝的温度发生了变化.参考该曲线,回答下列问题(不计电流表和电源的内阻).
图1所示为一个灯泡两端的电压与通过它的电流的变化关系曲线,可见两者不呈线性关系,这是由于焦耳热使灯丝的温度发生了变化.参考该曲线,回答下列问题(不计电流表和电源的内阻).| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| s2-s1 |
| 50(△t)2 |
| s2-s1 |
| 50(△t)2 |
| 1 |
| k |
| 1 |
| k |
| b |
| k |
| b |
| k |


| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| s3-s1 |
| 50△t2 |
| s3-s1 |
| 50△t2 |
| 1 |
| k |
| 1 |
| k |
| b |
| k |
| b |
| k |
14.D 15.BC 16.acd 17。AC 18。AD 19.ACD 20.ABD 21。BD
 22.
I..
4.945
22.
I..
4.945  650
650
II. (每空2分,图2分,共12分)
(a)滑片P位置不变(或保持R不变);调节电阻箱R1;
(b)r;
(c)5810;
(d)如图;3.4(或3.45或3.448).
23.解:
⑴小球在竖直方向做自由落体运动, (2分)
(2分)
水平方向做匀速直线运动  (2分)
(2分)
得: (1分)
(1分)
⑵设轨道半径为r,A到D过程机械能守恒:
 (3分)
(3分)
在A点: (2分)
(2分)
在D点: (2分)
(2分)
由以上三式得:
 (2分)
(2分)
由图象纵截距得:6mg=12 得m=
由L=
代入得:
r=
24.(18分)
(1)小球A受到向上的电场力Eq=0.05N (1分)
受到向上的洛仑兹力qvB=0.05N (1分)
受到向下的重力mg=0.1N (1分)
由于qE+qvB=mg (2分)
所以小球A和水平面之间的挤压力为零,因此小球A不受摩擦力作用,小球A向右做匀速直线运动. (2分)
小球A与小球B碰撞动量守恒定律mv0=-mv1+Mv2 (2分)
v2=
设小球B运动到圆轨道最高点的速度为v3,则根据机械能守恒定律得
Mv22/2=2mgR+Mv32/2 (2分)
小球B做平抛运动,则x=v3t (2分)
2R=gt2/2 (2分)
由以上各式联立解得:16R2-1.6R+x2=0 (2分)
R=
25.(1)线框在区域I中,P距O点x时,PQ切割磁感线产生的感应电动势为 (1分)
(1分)
MN切割磁感线产生的感应电动势为 (1分)
(1分)
线框中的感应电动势为 =
= =
= V (2分)
V (2分)
类似的,PQ在区域II中距中间边界 时,而MN在区域I中时,线框中的感应电动势为
时,而MN在区域I中时,线框中的感应电动势为
 =
= V (2分)
V (2分)
线框全部在区域II中,PQ距中间边界 时线框中的感应电动势为
时线框中的感应电动势为
 =
= V(2分)
V(2分)
由于线框匀速运动,故水平拉力做的功等于线框中产生的焦耳热,则


 =0.223J (2分)
=0.223J (2分)
(2)线圈运动时产生的平均感应电动势 ,
, ,电量
,电量 ,
,
联立化简得 (1分)
(1分)
设初速度为 ,右边框到达中间界线时速度为
,右边框到达中间界线时速度为 ,左边框到达中间界线时速度为
,左边框到达中间界线时速度为 ,则据动量定理有:
,则据动量定理有:
 (1分)
(1分)
 (1分)
(1分)
 (1分)
(1分)
其中 ,
, (2分)
(2分)
则 ,
(1分)
,
(1分)
故线框全部在在区域I运动时产生的热量为 (1分)
(1分)
线框全部在在区域II运动时产生的热量为 (1分)
(1分)
则 (1分)
(1分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com