练习册

  • 练习册
  • 试题
    15．对某型号1000只灯泡的使用寿命统计如下表所示:寿命分组 【查看更多】

     

    题目列表(包括答案和解析)

    （本小题共13分）

    在某校组织的一次篮球定点投篮训练中，规定每人最多投3次；在A处每投进一球得3分，在B处每投进一球得2分；如果前两次得分之和超过3分即停止投篮，否则投第三次，某同学在A处的命中率q为0.25，在B处的命中率为q，该同学选择先在A处投一球，以后都在B处投，用表示该同学投篮训练结束后所得的总分，其分布列为

    0

    2

    3

    4

    5

    p

    0.03

    P1

    P2

    P3

    P4

    (1)求q的值；

    (2)求随机变量的数学期望E;

    (3)试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小.

    查看答案和解析>>

    （本小题共13分）

    在某校组织的一次篮球定点投篮训练中，规定每人最多投3次；在A处每投进一球得3分，在B处每投进一球得2分；如果前两次得分之和超过3分即停止投篮，否则投第三次，某同学在A处的命中率q为0.25，在B处的命中率为q，该同学选择先在A处投一球，以后都在B处投，用表示该同学投篮训练结束后所得的总分，其分布列为

    0

    2

    3

    4

    5

    p

    0.03

    P1

    P2

    P3

    P4

    (1)求q的值；

    (2)求随机变量的数学期望E;

    (3)试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小.

    查看答案和解析>>

    （本小题满分13分）

    对某校高三年级学生参加社区服务次数进行统计，随机抽取名学生作为样本，得到这名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下：

    （Ⅰ）求出表中及图中的值；

    （Ⅱ）若该校高三学生有240人，试估计该校高三学生参加社区服务的次数在区间内的人数；

    （Ⅲ）在所取样本中，从参加社区服务的次数不少于20次的学生中任选2人，求至多一人参加社区服务次数在区间内的概率.

     

     

    分组

    频数

    频率

    10

    0.25

    24

     

     

    2

    0.05

    合计

    1

     

     

     

     

     

     

     

     

     

     

    查看答案和解析>>

    （本小题满分13分）对某校高一年级的学生参加社区服务的次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数，根据此数据作出了下图所示的频数与频率的统计表和频率分布直方图：

    （I）求出表中M、p及图中a的值

    （II）学校决定对参加社区服务的学生进行表彰，对参加活动次数在［25，30］区间的每个学生发放价值80元的学习用品，对参加活动次数在［20,25）区间的每个学生发放价值60元的学习用品，对参加活动次数在［15,20）区间的每个学生发放价值40元的学习用品，对参加活动次数在［10,15）区间的每个学生发放价值20元的学习用品，在所抽取的这M名学生中，任意取出2人，设X为此二人所获得学习用品价值之差的绝对值，求X的分布列与数学期望E（X）。

     

    查看答案和解析>>

    （本小题满分13分）

    对某校高三年级学生参加社区服务次数进行统计，随机抽取名学生作为样本，得到这名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下：

    分组

    频数

    频率

    10

    0.25

    24

     

     

    2

    0.05

    合计

    1

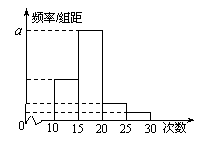
    （Ⅰ）求出表中及图中的值；

    （Ⅱ）若该校高三学生有240人，试估计该校高三学生参加社区服务的次数在区间内的人数；

    （Ⅲ）在所取样本中，从参加社区服务的次数不少于20次的学生中任选2人，求至多一人参加社区服务次数在区间内的概率.

    查看答案和解析>>

     

    1―5AACBB    6―8DCB

    二、填空题：本大题共6个小题，每小题5分，共30分。

    9．                10．                   11．6

    12．         13．①和③  或①和④             14．

    三、解答题：本大题共6个小题，共80分。

    15．解（I）该灯泡的使用寿命不足1500小时的概率 ……6分

       （II）至多有2只灯泡使用寿命不足1500小时的概率……12分

    答：从这1000只灯泡中任选1只灯泡使用寿命不足1500小时的概率等于

       从这1000只灯泡中任选3只，至多有2只灯泡使用寿命不足1500小时的概率等于。                                                  ……13分

    16．（本小题共13分）

    解：（I）由已知得          ……5分

        又在锐角△ABC中，所以A=60°，[不说明是锐角△ABC中，扣1分]……7分

       （II）因为a=2，A=60°所以  ……9分

        而                         ……11分

        又                        ……13分

        所以△ABC面积S的最大值等于

     

     

    17．（本小题共13分）

    解：（I）               ……3分

        由图知        ……5分

       （II）

                              ……6分

    令

    当

    故函数F（x）的单调增区间是，单调减区间  ……8分

    当故函数F（x）的单调增区间是……10分

    当a=0时，故函数F（x）的单调增区间是……12分

    综上所述：

    当函数F（x）的单调增区间是，单调减区间是。

    当时，函数F（x）的单调增区间是。              ……13分

    18．（本小题共14分）

    解：（I）在平面A’FA内过点 A’作A’H⊥垂足为H

        因为    ……4分

        所以               ……6分

        即点A′在平面ABC上的射影在线段AF上         ……7分

      （II）由（I）知，又A′E……9分

     

     

       则点H为正

       因为……11分

    而，所以二面角的大小为……13分

    二面角的大小即为当所旋转过的角的大小。

    故所求角等于                                          ……14分

    19．（本小题共14分）

        解：（I）由已知……2分

         ……5分

    所以当有最小值为-7；

         当有最大值为1。                        ……7分

       （II）设点  直线AB方程：

             ……※

    有 ……9分

    因为为钝角，

    所以    ……12分

    解得，此时满足方程※有两个不等的实根……14分

    故直线l的斜率k的取值范围  

     

    20．（本小题共14分）

    解：（I）因为数列是等差数列，公差为2

       

        （II）又

    ，与已知矛盾，所以3

    当时，  所以=4  ……8分

        （III）由已知当=4时，

    令

    所以数列{an}的前n项和

       

    ……14分

     

     


    同步练习册答案