
题目列表(包括答案和解析)
 是等差数列,公差为2,a1,=11,an+1=λan+bn.
是等差数列,公差为2,a1,=11,an+1=λan+bn. 的值;
的值;已知数列![]() 是等差数列,其前
是等差数列,其前![]() 项和为
项和为![]() ,
,![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)求![]() 的最小值及此时
的最小值及此时![]() 的值
的值
(16分)已知数列 是等差数列,
是等差数列,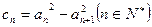
(1)判断数列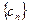 是否是等差数列,并说明理由;
是否是等差数列,并说明理由;
(2)如果 ,试写出数列
,试写出数列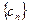 的通项公式;
的通项公式;
(3)在(2)的条件下,若数列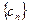 得前n项和为
得前n项和为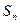 ,问是否存在这样的实数
,问是否存在这样的实数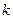 ,使
,使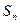 当且仅当
当且仅当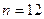 时取得最大值。若存在,求出
时取得最大值。若存在,求出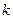 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
已知数列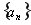 是等差数列,
是等差数列,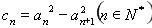
(1)判断数列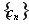 是否是等差数列,并说明理由;
是否是等差数列,并说明理由;
(2)如果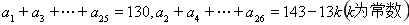 ,试写出数列
,试写出数列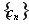 的通项公式;
的通项公式;
(3)在(2)的条件下,若数列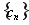 得前n项和为
得前n项和为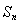 ,问是否存在这样的实数
,问是否存在这样的实数 ,使
,使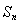 当且仅当
当且仅当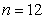 时取得最大值。若存在,求出
时取得最大值。若存在,求出 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
已知数列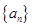 是等差数列,且
是等差数列,且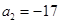 ,
,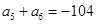 ;又若
;又若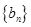 是各项为正数的等比数列,且满足
是各项为正数的等比数列,且满足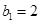 ,其前
,其前 项和为
项和为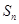 ,
,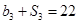 .
.
(1)分别求数列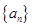 ,
,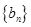 的通项公式
的通项公式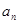 ,
,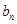 ;
;
(2)设数列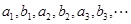 的前
的前 项和为
项和为 ,求
,求 的表达式,并求
的表达式,并求 的最小值.
的最小值.
1―5AACBB 6―8DCB
二、填空题:本大题共6个小题,每小题5分,共30分。
9.  10.
10. 11.6
11.6
12. 13.①和③ 或①和④
14.
13.①和③ 或①和④
14.
三、解答题:本大题共6个小题,共80分。
15.解(I)该灯泡的使用寿命不足1500小时的概率 ……6分
……6分
(II)至多有2只灯泡使用寿命不足1500小时的概率 ……12分
……12分
答:从这1000只灯泡中任选1只灯泡使用寿命不足1500小时的概率等于
从这1000只灯泡中任选3只,至多有2只灯泡使用寿命不足1500小时的概率等于 。
……13分
。
……13分
16.(本小题共13分)
解:(I)由已知得 ……5分
……5分
又在锐角△ABC中,所以A=60°,[不说明是锐角△ABC中,扣1分]……7分
(II)因为a=2,A=60°所以 ……9分
……9分
而 ……11分
……11分
又 ……13分
……13分
所以△ABC面积S的最大值等于
17.(本小题共13分)
解:(I) ……3分
……3分
由图知 ……5分
……5分
(II)
 ……6分
……6分

令
当
故函数F(x)的单调增区间是 ,单调减区间
,单调减区间 ……8分
……8分
当 故函数F(x)的单调增区间是
故函数F(x)的单调增区间是 ……10分
……10分
 当a=0时,
当a=0时, 故函数F(x)的单调增区间是
故函数F(x)的单调增区间是 ……12分
……12分
综上所述:
当 函数F(x)的单调增区间是
函数F(x)的单调增区间是 ,单调减区间是
,单调减区间是 。
。
当 时,函数F(x)的单调增区间是
时,函数F(x)的单调增区间是 。
……13分
。
……13分
18.(本小题共14分)
解:(I)在平面A’FA内过点 A’作A’H⊥垂足为H
因为 ……4分
……4分
所以
 ……6分
……6分
即点A′在平面ABC上的射影在线段AF上 ……7分
(II)由(I)知 ,又A′E
,又A′E ……9分
……9分
则点H为正
因为 ……11分
……11分
而 ,所以二面角
,所以二面角 的大小为
的大小为 ……13分
……13分
二面角 的大小即为当
的大小即为当 所旋转过的角的大小。
所旋转过的角的大小。
故所求角等于 ……14分
……14分
19.(本小题共14分)
解:(I)由已知 ……2分
……2分
 ……5分
……5分
所以当 有最小值为-7;
有最小值为-7;
当 有最大值为1。
……7分
有最大值为1。
……7分
(II)设点 直线AB方程:
直线AB方程:
 ……※
……※
有 ……9分
……9分
因为 为钝角,
为钝角,
所以 ……12分
……12分
解得 ,此时满足方程※有两个不等的实根……14分
,此时满足方程※有两个不等的实根……14分
故直线l的斜率k的取值范围 
20.(本小题共14分)
解:(I)因为数列 是等差数列,公差为2
是等差数列,公差为2

(II)又
 ,与已知矛盾,所以
,与已知矛盾,所以 3
3
当 时,
时, 所以
所以 =4 ……8分
=4 ……8分
(III)由已知 当
当 =4时,
=4时,
令

所以数列{an}的前n项和

……14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com