题目列表(包括答案和解析)
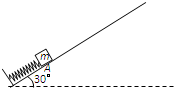
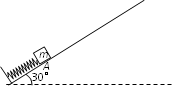
如图所示，倾角为30°的光滑斜面，底端固定一沿斜面方向的弹簧．一质量为m的滑块将弹簧压缩到A点（滑块与弹簧不连接），此时弹簧的压缩量为△L．滑块在A点由静止释放，沿斜面滑过距离L时速度为0．求：如图所示，倾角为30°的光滑斜面，底端固定一沿斜面方向的弹簧．一质量为m的滑块将弹簧压缩到A点(滑块与弹簧不连接)，此时弹簧的压缩量为ΔL．滑块在A点由静止释放，沿斜面滑过距离L时速度为0．求：
(1)滑块在A点时弹簧的弹性势能；
(2)滑块刚脱离弹簧时的速度．
如图所示，倾角为30°的光滑斜面的下端有一水平传送带．传送带正以v=6m/s的速度运动，运动方向如图所示．一个质量为2㎏的物体（物体可以视为质点），从h=3.2m高处由静止沿斜面下滑，物体经过A点时，无论是从斜面到传送带还是从传送带到斜面，都不计其速率变化．物体与传送带间的动摩擦因数为0.5，传送带左右两端A、B间的距离LAB=10m，重力加速度g=10m/s2，则：
如图所示，倾角为30°的光滑斜面的下端有一水平传送带，传送带正以6m/s的速度运动，运动方向如图所示．一个质量为2kg的物体（物体可以视为质点），从h=3.2m高处由静止沿斜面下滑，物体经过A点时，不管是从斜面到传送带还是从传送带到斜面，都不计其动能损失．物体与传送带间的动摩擦因数为0.5，物体向左最多能滑到传送带左右两端AB的中点处，重力加速度g=10m/s2，求：一、单项选择题：本题共5小题，每小题3分，共计15分
题号
1
2
3
4
5
答案
A
B
D
B
C
二、多项选择题：每小题4分，共计16分。每小题有多个选项符合题意，全部选对的得4分，选对但不全的得2分，错选或不答的得O分。
题号
6
7
8
9
答案
BD
AD
ACD
BD
三、简答题：本题分必做题（第l0、11题)和选做题(第12题)两部分，共计42分。请将解答填写在答题卡相应的位置。
10．⑴探究的是加速度与其它量之间的比例关系(其它答法只要正确就给分。如：初速度为零的匀加速运动，在相同的时间内，位移与加速度成正比) （3分）
⑵砝码的数量 （2分） ⑶
a(或
)（2分）、（或a）（2分）
11．⑴g 导线（3分） ⑵0.8（3分）
⑶AC（3分）（错选得0分，漏选得2分）
12．
A（3-3）⑴AD（3分）（错选得0分，漏选得2分）
⑵BD（3分）（错选得0分，漏选得2分）
⑶解：由热力学第一定律△U=W+Q得
△U=（F+mg+P0S）△h－Q （6分）
B（3-4）⑴
⑵AB （3分）（错选得0分，漏选得2分）
⑶解：∵n=
∴r=300 （2分）
光路图如右图所示
∴L1=d/cosr =
（2分）
∴L2= L1sin300=
（2分）
C（3-5）⑴
（3分）
⑵D（3分）
⑶解：由图知
=
=―
=
根据动量守恒定律有：ma =ma + mb （2分）
∴mb=
四、计算题：本题共4小题，共计47分。解答时请写出必要的文字说明、方程式和重要的演算步骤，只写出最后答案的不能得分。有数值计算的题，答案中必须明确写出数值和单位。
13．解：
⑴
（4分）
⑵
（4分）
14．解：
⑴ △x = aT2 ∴a = △x/
T2
=
=
⑵
= 
=
⑶ h =
∴t=
=4s
（2分）
BC = bc + 
t －
t
（2分）
= bc + (－)t
= bc + aTt
=
15．解：
⑴负电荷 （3分）
⑵刚进入磁场瞬间，由牛顿第二定律得：
F合 = qkt－μ(mg + Bqv)=ma ① （2分）
进入磁场△t瞬间，由牛顿第二定律得：
F′合 = qk(t+△t)－μmg－μ Bq(
+a△t)=ma ② （2分）
解①②得：a=
③ （2分）
⑶ ③式代入①式得：t=
+
+
④ （2分）
E=kt=
⑤ （1分）
16．解：
⑴进入磁场瞬间回路中动生电动势E1=
= kLgt12 （2分）
感生电动势E2=S
=Ldk （2分）
∵回路电流为零，∴动生电动势E1与感生电动势E2方向相反、大小相等，即：
E1 = kLgt12 = E2 = Ldk
∴d = gt1 2 （1分）
⑵Q=
=
=
（3分）
⑶金属棒在L1上方电流I1 = 
= 
（1分）
金属棒穿出磁场前瞬间电流I2 = 
= 
=
（1分）
∵I1= I2
∴
=
（2分）
金属棒穿过磁场过程中，由动能定理得：
mgd－W=
－
（2分）
W= mgd+
－
=
（1分）
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com