
题目列表(包括答案和解析)
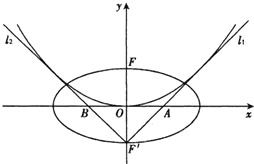 已知椭圆E的中心在原点,焦点在x轴上,离心率为
已知椭圆E的中心在原点,焦点在x轴上,离心率为
| ||
| 2 |
| ||
| 2 |
| 2 |
| MQ |
| QF |
已知椭圆E的中心在原点,焦点在x轴上,椭圆上的点到焦点的距离的最小值为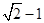 ,离心率e=
,离心率e=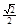 .
.
(Ⅰ) 求椭圆E的方程;
(Ⅱ) 过点(1,0)作直线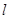 交E于P、Q两点,试问在x轴上是否存在一定点M,使
交E于P、Q两点,试问在x轴上是否存在一定点M,使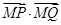 为定值?若存在,求出定点M的坐标;若不存在,请说明理由.
为定值?若存在,求出定点M的坐标;若不存在,请说明理由.
已知椭圆E的中心在原点,焦点在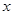 轴上,椭圆上的点到两个焦点的距离之和为
轴上,椭圆上的点到两个焦点的距离之和为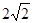 ,离心率
,离心率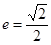
(1)求椭圆E的方程;
(2)作直线l: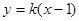 交椭圆E于点P、Q,且OP^OQ。求实数k的值.
交椭圆E于点P、Q,且OP^OQ。求实数k的值.
已知椭圆E的中心在原点,焦点在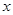 轴上,椭圆上的点到两个焦点的距离之和为
轴上,椭圆上的点到两个焦点的距离之和为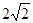 ,离心率
,离心率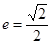
(1)求椭圆E的方程;
(2)作直线l: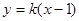 交椭圆E于点P、Q,且OP^OQ。求实数k的值.
交椭圆E于点P、Q,且OP^OQ。求实数k的值.
一、选择题:本大题共12小题,每小题5分,满分60分。
1.C 2.D 3.A 4.B 5.A 6.D 7.B 8.C 9.A
10.B 11.D 12.C
二、填空题:本大题共4小题,每小题5分,满分20分。
13.64 14. 15.4 16.
15.4 16.
三、解答题:本大题共6小题,满分70分。
17.(本小题满分10分)
(1)解:∵ 2分
2分
∴
∴
∴ 5分
5分
(2)解:∵
∴
又∵ 7分
7分
∵ ,
,
∵
= 10分
10分
18.(本小题满分12分)
解:用Ai表示事件:一天之内第i个部件需要调整(i=1、2、3),
则 ,
,
用 表示一天之内需要调整的部件数,则
表示一天之内需要调整的部件数,则
(1) ……3分
……3分
(2)
 ……………………12分
……………………12分
答:一天之内恰有一个部件需要调整的概率是0.398;一天之内至少有两个部件需要调整的概率是0.098.
19.(本小题满分12分)
解法一:
(1)证明:在直三棱柱ABC―A1B
|