题目列表(包括答案和解析)
已知数列
的前
项和为
，且
(
N*),其中
．
(Ⅰ) 求的通项公式；
(Ⅱ) 设
(
N*).
①证明： 
；
② 求证：
.
【解析】本试题主要考查了数列的通项公式的求解和运用。运用
关系式，表示通项公式，然后得到第一问，第二问中利用放缩法得到
，②由于
，
所以
利用放缩法，从此得到结论。
解：(Ⅰ)当
时，由
得
. ……2分
若存在
由
得
，
从而有
，与矛盾，所以
.
从而由得
得
. ……6分
(Ⅱ)①证明：
证法一：∵
∴
∴
∴
.…………10分
证法二：
，下同证法一.
……10分
证法三：（利用对偶式）设
，
，
则
.又
，也即
，所以
，也即
，又因为
，所以
.即
………10分
证法四：（数学归纳法）①当
时, 
,命题成立;
②假设
时,命题成立,即
,
则当
时,
即
即
故当时，命题成立.
综上可知，对一切非零自然数，不等式②成立. ………………10分
②由于，
所以，
从而
.
也即
已知数列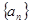
满足
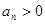且对一切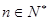
,
有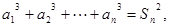
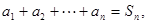
（Ⅰ）求证：对一切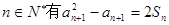
（Ⅱ）求数列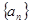通项公式.
（Ⅲ）求证：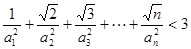
【解析】第一问利用，已知表达式，可以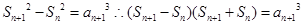得到
，然后得到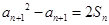
，从而求证
。
第二问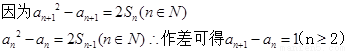
，可得数列的通项公式。
第三问中，利用放缩法的思想，我们可以得到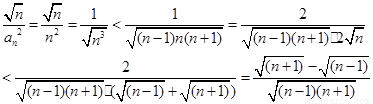
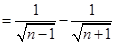然后利用累加法思想求证得到证明。
解: (1) 证明:
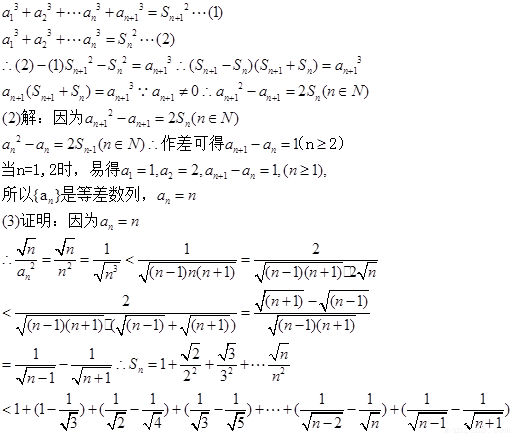
已知，如图，AB是⊙O的直径，AC切⊙O于点A，AC=AB，CO交⊙O于点P，CO的延长线交⊙O于点F， BP的延长线交AC于点E.
⑴求证：FA∥BE；
⑵求证：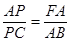
【解析】本试题主要是考查了平面几何中圆与三角形的综合运用。
（1）要证明线线平行，主要是通过证明线线平行的判定定理得到
（2）利用三角形△APC∽△FAC相似，来得到线段成比列的结论。
证明：（1）在⊙O中，∵直径AB与FP交于点O ∴OA=OF
∴∠OAF=∠F ∵∠B=∠F ∴∠OAF=∠B ∴FA∥BE
（2）∵AC为⊙O的切线，PA是弦 ∴∠PAC=∠F
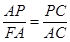
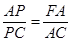∵∠C=∠C ∴△APC∽△FAC ∴
∴
∵AB=AC
∴
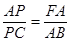
已知数列
的前n项和
且
=2.
（1） 求
的值,并证明：当n>2时有
；
（2） 求证：
…
.
【解析】本试题主要是考查了数列中通项公式与前n项和关系式的运用。得到数列相邻两项之间的关系式。同时能利用的通项公式，求解前n项和，并求和证明。
已知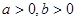
，求证：
.
【解析】本试题主要是考查了不等式的证明，利用分析法进行变形化简并证明。
一、填空题
1. 二 2. 6 3.
4. 22 5.
{2,3,4} 6. 5049 7.
8. 2 9. 
10. 5 11. 
12.
13. 4 14. 
二．解答题
15. 解：设四发子弹编号为0（空弹），1，2，3，
（1）设第一枪出现“哑弹”的事件为A，有4个基本事件,则：（2分）
（4分）
(2)
法一:前三枪出现“哑弹”的事件为B,则第四枪出现“哑弹”的事件为
,
那么
，（6分）
（9分）
法二:前三枪共有4个基本事件{0,1,2},{0,1,3},{0,2,3},{1,2,3},满足条件的有三个,（7分）
则
（9分）
(3) 
的面积为6，（10分）
分别以
为圆心、1为半径的三个扇形的面积和
,（12分）
设第四个弹孔与前三个弹孔的距离都超过1的事件为C,
.（14分）
16.
（1）
ABCD为直角梯形，AD =
，
AB⊥BD，（1分）
PB⊥BD ，AB
PB =B，AB，PB
平面PAB，BD⊥平面PAB，（ 4分）
PA面PAB，PA ⊥BD.（5分）
（2）假设PA=PD,取AD 中点N,连PN,BN,则PN⊥AD，BN⊥AD, （7分）
AD⊥平面PNB,得 PB⊥AD，（8分）
又PB⊥BD ，得PB⊥平面ABCD,
∴
（9分）
又∵
，∴CD⊥平面PBC,
∴CD⊥PC, 与已知条件
与
不垂直矛盾
∴
（10分）
（3）在上l取一点E，使PE=BC，（11分）
PE∥BC，四边形BCPE是平行四边形，（12分）
PC∥BE，PC
平面EBD， BE平面EBD
PC∥平面EBD.（14分）
17. 解：⑴∵椭圆C的短轴长为2，椭圆C的一条准线为l：
，
∴不妨设椭圆C的方程为
．（2分）
∴
，（ 4分） 即
．（5分）
∴椭圆C的方程为
．（6分）
⑵ F（1，0），右准线为l：， 设
，
则直线FN的斜率为
，直线ON的斜率为
，（8分）
∵FN⊥OM，∴直线OM的斜率为
，（9分）
∴直线OM的方程为：
，点M的坐标为
．（11分）
∴直线MN的斜率为
．（12分）
∵MN⊥ON，∴
，
∴
，
∴
，即
．（13分）
∴
为定值．（14分）
18. 解：（1）设
，则
．（2分）
在Rt△MB
中，
， （4分）
∴
． （5分）
∵点M在线段AB上，M点和B点不重合，
点和B点不重合，
∴
．（7分）
（2）在△AMN中，∠ANM＝
,（8分）
,（9分）
＝
．（10分）
令
＝
＝
．（13分）
∵， ∴
． （14分）
当且仅当
，
时，
有最大值
，（15分）
∴时，
有最小值
．（16分）
19.（1）如果
为偶函数，则
恒成立，（1分）
即：
（2分）
由
不恒成立，得
（3分）
如果为奇函数，则
恒成立，（4分）
即：
（5分）
由
恒成立，得
（6分）
（2）
，
∴ 当
时,显然
在R上为增函数；（8分）
当
时，
，
由
得
得
得
.（9分）
∴当
时, 
,为减函数; （10分）
当
时, 
,为增函数. （11分）
(3) 当
时，
如果
，（13分）
则
∴函数
有对称中心
（14分）
如果
（15分）
则
∴函数有对称轴
.（16分）
20. 解：（1）n＝1时，
． （1分）
n≥2时，2Sn＝anan＋1＋r，① 2Sn－1＝an－1an＋r，②
①－②，得2an＝an(an＋1－an－1)．∵an≠0，∴an＋1－an－1＝2． （ 3分）
则a1，a3，a5，…，a2n－1，… 成公差为2的等差数列，a2n－1＝a1＋2(n－1)．
a2，a4，a6，…，a2n，… 成公差为2的等差数列， a2n＝a2＋2(n－1)．
要使{an}为等差数列，当且仅当a2－a1＝1．即
．r＝c－c2． （ 4分）
∵r＝－6，∴c2－c－6＝0，c＝－2或3．
∵当c＝－2，
，不合题意，舍去.
∴当且仅当
时，数列
为等差数列 （5分）
（2）
＝[a1＋2(n－1)]－[a2＋2(n－1)]＝a1－a2＝
－2．
＝[a2＋2(n－1)]－（a1＋2n）＝a2－a1－2＝－()． （8分）
∴
（9分）
． （10分）
＝
．（11分）
∵r＞c＞4，∴
＞4，∴
＞2．
∴0＜
＜1． （13分）
且
＞－1． （14分）
又∵r＞c＞4，∴
，则0＜
．
．
∴
＜1．
．∴
＜1．（15分）
∴对于一切n∈N*，不等式
恒成立．（16分）
数学加试题参考答案及评分标准
21．A．选修4―1 几何证明选讲
证明:作
于
为直径,
（2分）
四点共圆,
四点共圆. （6分）
（8分）
(1)+(2)得
（9分）
即
（10分）
21．B．选修4―2 矩阵与变换
解：（1）由
=
，（2分） ∴
. （3分）
（2）由（1）知
，则矩阵的特征多项式为
（5分）
令
，得矩阵
同步练习册答案
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com