练习册

  • 练习册
  • 试题
    整数.点在给定的函数的图像上.若,点()和点与点构成一个以为顶点的等腰三角形. 【查看更多】

     

    题目列表(包括答案和解析)

    给出定义：若 (其中为整数)，则叫做离实数最近的整数，记作，即. 在此基础上给出下列关于函数的四个命题：①的定义域是，值域是；

    ②点是的图像的对称中心；③函数的最小正周期为1；

    ④ 函数在上是增函数；  则其中真命题是_   ．

    查看答案和解析>>

    给出定义：若 (其中为整数)，则叫做离实数最近的整数，记作，即. 在此基础上给出下列关于函数的四个命题：

    ①的定义域是，值域是；

    ②点是的图像的对称中心；

    ③函数的最小正周期为1；

    ④ 函数在上是增函数； 

    则其中真命题是_   ．

    查看答案和解析>>

    给出定义：若(其中m为整数)，则m叫做离实数x最近的整数，记作{x}，即{x}＝m，在此基础上给出下列关于函数f(x)＝x－{x}的四个命题：

    ①y＝f(x)的定义域是R，值域是；

    ②点的图像的对称中心；

    ③函数上是增函数；

    ④函数y＝f(x)的最小正周期为1；

    则其中真命题是________．

    查看答案和解析>>

    给出定义：若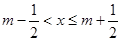（其中m为整数），则m叫做离实数x最近的整数，记作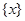，即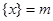，在此基础上给出下列关于函数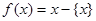的四个命题：

    ①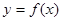的定义域是R，值域是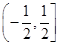；②点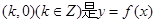的图像的对称中心；③函数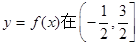上是增函数；  ④函数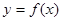的最小正周期为1；

     则其中真命题是         

     

    查看答案和解析>>

    给出定义：若 (其中为整数)，则叫做离实数最近的整数，记作，即. 在此基础上给出下列关于函数的四个命题：

    ①的定义域是，值域是；

    ②点是的图像的对称中心，其中；

    ③函数的最小正周期为；

    ④ 函数在上是增函数．

    则上述命题中真命题的序号是             ．

    查看答案和解析>>

    一、选择题1B   2C   3D   4B  5A  6C   7D   8A   9A   10B  11B   12 A

     

    二、填空题13、高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。   14、4    ；15、高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。16、高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。或 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    三、解答题

    17．（10分）

    解：（I）高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,即高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时, 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。取得最大值高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。.

    函数高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的取得最大值的自变量高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的集合为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。…………5分

     (II)高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。由题意得: 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    即 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。又由高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。因此函数高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的单调减区间为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。.……10分

    18.（12分）解：（I）高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。 ………………4分

           (II)ξ可取1，2，3，4.

        高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，

        高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。； …………8分

        故ξ的分布列为

    ξ

    1

    2

    3

    4

    P

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

                                ……………………………………………………………10分

        高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。………………………12分

     

    19.解：（Ⅰ）取BC中点F，连结AF，则CF＝AD，且CF∥AD，

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。∴四边形ADCF是平行四边形，∴AF∥CD，

    ∴∠PAF（或其补角）为异面直线PA与CD所成的角　………………………  2分

    ∵PB⊥平面ABCD，∴PB⊥BA，PB⊥BF．

    ∵PB＝AB＝BF＝1，∴AB⊥BC，∴PA＝PF＝AF＝高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。．　

    ∴△PAF是正三角形，∠PAF＝60°　

    即异面直线PA与CD所成的角等于60°．………4分                                   

    （Ⅱ）在Rt△PBD中，PB＝1，BD＝高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，∴PD＝高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    ∵DE＝2PE，∴PE＝

    则高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，∴△PBE∽△PDB，∴BE⊥PD．　……………………     5分

    由（Ⅰ）知，CF＝BF＝DF，∴∠CDB＝90°．

    ∴CD⊥BD．又PB⊥平面PBD，∴PB⊥CD．

    ∴CD⊥平面PBD，∴CD⊥BE　…………………………7分

    ∴BE⊥平面PCD．　………………………………………8分

    （Ⅲ）连结AF，交BD于点O，则AO⊥BD．

    ∵PB⊥平面ABCD，∴平面PBD⊥平面ABD，∴AO⊥平面PBD．

    过点O作OH⊥PD于点H，连结AH，则AH⊥PD．

    ∴∠AHO为二面角A－PD－B的平面角．　…………………………………     10分

    在Rt△ABD中，AO＝．

    在Rt△PAD中，AH＝高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。．　

    在Rt△AOH中，sin∠AHO＝高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。．∴∠AHO＝60°．    

    即二面角A－PD－B的大小为60°………………………………………12分

    20.（12分）

    解：高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。……2分

    令高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。=0，得 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    （1）当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    即高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。<0或高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。>4时高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。有两个不同的实根高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，不妨设高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。<高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    于是高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，从而有下表

     

     

    x

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    x1

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    +

    0

    －

    0

    +

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    ↑

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。为极大值

    ↓

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。为极小值

    ↑

    即此时高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。有两个极值点. ………6分

    （2）当△=0即高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。=0或高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。=4时，方程高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。有两个相同的实根高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。于是高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。………                       8分

    故当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。<高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。>0，当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。>高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。>0，因此高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。无极值………10分

    （3）当△<0即0<高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。<4时高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，故高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。为增函数，此时高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。无极值.

    综上，当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。无极值点

    ………  12分

    21.解：（Ⅰ）设： 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，则高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，因为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，所以高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的最小值为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，又高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，故双曲线高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的方程为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。.                                            -----------------4分

    （Ⅱ）由高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。可知高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，相应准线为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，设过高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的直线为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，

    代入高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。中，消去高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。可得，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。????①

    由题意知高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，设高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，则高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。是方程①的两个根，由韦达定理，得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。将两式相除，得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    因高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，故直线高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的斜率为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    ???????????8分

    所以，直线高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的方程为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，将高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。代入方程中，整理可得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，所以直线高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。恒过定点高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。.    ???????12分                          

    22. 解：（Ⅰ）由高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。得 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。.当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，因为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。构成以高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。为顶点的等腰三角形,所以

           高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

           又因为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。在函数高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的图像上，所以高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。.(高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。)

      又点高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的坐标满足前式，所以高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

     （Ⅱ）因为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,所以高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

           设高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,则高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。.①

           所以 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。②

           由①和②得:高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。.

           所以高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

       高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。<3…………………8分

           （Ⅲ）由已知得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。对一切高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。均成立.

           所以高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

           高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。>1

           所以高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。单调递增.最小值为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。.

    又因为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。对一切高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。均成立.所以高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。.高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。………………   12分

     

     


    同步练习册答案