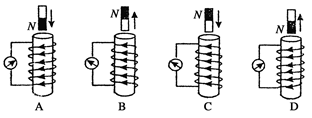
1.3.5
二、本体共3小题，共18分。把答案填在题中的横线上。
11．（1）6×103；（2）36.0；（3）180（各2分）
12．（1）小车与滑轮之间的细线水平（或与轨道平行）（2分）；远小于（2分）
（2）两车从静止开始作匀加速直线运动，且两车的运动时间相等，据S= aT2知，S与a成正比（2分）
13．（1）2.98（3分）；（2）5.0（3分）
三、本题共5小题，共42分。解答写出必要的文字说明、方程式和重要的演算步骤。只写出最后答案的不能得分。有数值计算的题，答案中必须明确写出数值和单位。
14．（8分）解答：
两球发生弹性碰撞，设碰后甲、乙两球的速度分别为v1、v2，则
m1v0 = m1v1 + m2v2 2分
m1v02 = m1v12 + m2v22 2分
从两球碰撞后到它们再次相遇，甲和乙的速度大小保持不变，由于BC=2AB，则甲和乙通过的路程之比为1：5，故碰撞后甲和乙的速度之比为，
v1:v2
= 1:5 2分
联立解得 = 2分
15．（8分）解答：
（1）设A、B两物块的加速度为a1、a2，由v―t图得
a1 = = m/s2 = m/s2 1分
a2 = = m/s2 = － m/s2 1分
分别以A、B为研究对象，摩擦力大小为f，由牛顿第二定律
F－f = ma1 1分
－f = ma2 1分
联立解得 F = 0.8N 1分
（2）设A、B在12s内的位移分别为S1、S2，由v―t图得
S1 = ×（4 + 8）×12m = 72m 1分
S2 = ×6×4m = 12m 1分
故S = S1－S2 = 60m 1分
16．（8分）解答：
（1）设带电粒子射入磁场时的速度大小为v，由带电粒子射入匀强磁场的方向和几何关系可知，带电粒子在磁场中做圆周运动，圆心位于坐标原点O，半径为l。
则Bqv = m ①1分
设带电粒子在磁场中运动时间为t1，在电场中运动的时间为t2，总时间为t。
t1 = T ②1分
T = ③1分
t2 = ④1分
联立解得 t = 1分
（2）带电粒子在电场中做类平抛运动，设加速度为a，则
l = at22 ⑤1分
a = ⑥1分
联立①④⑤⑥解得 E
= 1分
17．（8分）解答：
设绳中张力为T，斜面对A的支持力为NA，A、B加速度大小为a，以A为研究对象，
由牛顿第二定律
mAgsin37° －T =ma ①2分
NA = mAgcos37°④ ②1分
以B为研究对象，由牛顿第二定律
T－mBg = mBa ③2分
联立解得 a = 2m/s2 T
= 12N NA= 24N
以斜面体为研究对象，受力分析后，在水平方向
F = N′Asin37°－Tcos37° ④2分
NA = N′A
解得 F = 4.8N 1分
（或以整体为研究对象，由牛顿第二定律得F = mAacos37°）=4.8N，则本式给4分，①③式各给2分，共8分）
18．（10分）解答：
（1）当小物块速度小于3m/s时，小物块受到竖直向下的重力、垂直传送带向上的支持力和沿传送带斜向下的摩擦力作用，做匀加速直线运动，设加速度为a1，根据牛顿第二定律
mgsin30° + μmgcos30°=ma1 ①1分
解得 a1 = 7.5m/s2
当小物块速度等于3m/s时，设小物块对地位移为L1，用时为t1，根据匀加速直线运动规律
t1 = ②1分
L1 = ③1分
解得 t1 =
0.4s L1 = 0.6m
由于L1＜L 且μ＜tan30°，当小物块速度大于3m/s时，小物块将继续做匀加速直线运动至B点，设加速度为a2，用时为t2，根据牛顿第二定律和匀加速直线运动规律
mgsin30°－μmgcos30°=ma2 ④1分
解得 a2
= 2.5m/s2
L－L1 = v1t2 + a2t22 ⑤1分
解得 t2 =
0.8s
故小物块由禁止出发从A到B所用时间为 t = t1 + t2 = 1.2s 1分
（2）作v―t图分析知：传送带匀速运动的速度越大，小物块从A点到B点用时越短，当传送带速度等于某一值v′ 时，小物块将从A点一直以加速度a1做匀加速直线运动到B点，所用时间最短，即
L = a1tmin2 ⑥1分
解得tmin = 1s
v′ =a1tmin =7.5m/s
此时小物块和传送带之间的相对路程为 △S = v′
t－L = 3.75m
传送带的速度继续增大，小物块从A到B的时间保持不变，而小物块和传送带之间的相对路程继续增大，小物块在传送带上留下的痕迹也继续增大；当痕迹长度等于传送带周长时，痕迹为最长Smax，设此时传送带速度为v2，则
Smax = 2L + 2πR ⑦1分
Smax = v2t－L ⑧1分
联立⑥⑦⑧解得 v2 = 12.25m/s 1分
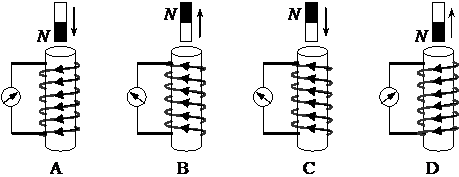
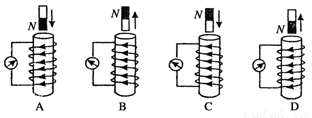
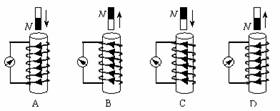
标出了磁
铁的极性、磁铁相对线圈的运动方向以及线圈中产生的感应电流的
方向等情况，其中正确的是 ( )