1.3.5
第Ⅱ卷(非选择题,共100分)
二、填空题
11.4 12.96 13.-3 14.(文) (理)
(理)
15.(文) (理)
(理)
三、解答题
16.解:(1)




 …………(4分)
…………(4分)
(1)(文科)在 时,
时,


在 时,
时, 为减函数
为减函数
从而 的单调递减区间为
的单调递减区间为 ;…………(文8分)
;…………(文8分)
(2)(理科)

当 时,由
时,由 得单调递减区间为
得单调递减区间为
同理,当 时,函数的单调递减区间为
时,函数的单调递减区间为 …………(理8分)
…………(理8分)
(3)当 ,变换过程如下:
,变换过程如下:
1°将 的图象向右平移
的图象向右平移 个单位可得函数
个单位可得函数 的图象。
的图象。
2°将所得函数图象上每个点的纵坐标扩大为原来的 倍,而横坐标保持不变,可得函数
倍,而横坐标保持不变,可得函数 的图象。
的图象。
3°再将所得图象向上平移一个单位,可得 的图象……(12分)
的图象……(12分)
(其它的变换方法正确相应给分)
17.解:(1) 三棱柱ABC―A1B1C1为直三棱柱
三棱柱ABC―A1B1C1为直三棱柱
 底面ABC
底面ABC
又 AC
AC 面ABC
面ABC
 AC
AC
又

又 AC
AC 面B1AC
面B1AC
 …………(6分)
…………(6分)
(2) 三棱柱ABC―A1B1C1为直三棱柱
三棱柱ABC―A1B1C1为直三棱柱
 底面ABC
底面ABC
 为直线B1C与平面ABC所成的角,即
为直线B1C与平面ABC所成的角,即
过点A作AM⊥BC于M,过M作MN⊥B1C于N,加结AN。
∴平面BB1CC1⊥平面ABC
∴AM⊥平面BB1C1C
由三垂线定理知AN⊥B1C从而∠ANM为二面角B―B1C―A的平面角。
设AB=BB1=
在Rt△B1BC中,BC=BB1

即二面角B―B1C―A的正切值为 …………(文12分)
…………(文12分)
(3)(理科)过点A1作A1H⊥平面B1AC于H,连结HC,则
∠A1CH为直线A1C与平面B1AC所成的角
由 知
知

在Rt ………………(理12分)
………………(理12分)
18.解:(文科)(1)从口袋A中摸出的3个球为最佳摸球组合即为从口袋A中摸出2个红球和1个黑球,其概率为
 ………………………………(6分)
………………………………(6分)
(2)由题意知:每个口袋中摸球为最佳组合的概率相同,从5个口袋中摸球可以看成5次独立重复试难,故所求概率为
 ……………………………………(12分)
……………………………………(12分)
(理科)(1)设用队获第一且丙队获第二为事件A,则
 ………………………………………(6分)
………………………………………(6分)
(2) 可能的取值为0,3,6;则
可能的取值为0,3,6;则
甲两场皆输:
甲两场只胜一场:
|

0 3 6 P 


 的分布列为 的分布列为
 …………………………(12分) …………………………(12分) 19.解:(文科)(1)由 函数 的定义域为(-1,1) 的定义域为(-1,1) 又   …………………………………(6分) …………………………………(6分)
(2)任取 、 、    又  ……(13分) ……(13分)
(理科)(1)由  又由函数 
当且仅当 即 即  综上 …………………………………………………(6分) …………………………………………………(6分)
(2)  


① ②令 综上所述实数m的取值范围为 ……………(13分) ……………(13分) 20.解:(1) 的解集有且只有一个元素 的解集有且只有一个元素  又由  当 当   …………………………………(文6分,理5分) …………………………………(文6分,理5分)
(2) ① ①  ② ②
由①-②得  …………………………………………(文13分,理10分) …………………………………………(文13分,理10分)
(3)(理科)由题设  综上,得数列 共有3个变号数,即变号数为3.……………………(理13分) 共有3个变号数,即变号数为3.……………………(理13分) 21.解(1)   ………………………………(文6分,理4分)(2)(2)当AB的斜率为0时,显然 ………………………………(文6分,理4分)(2)(2)当AB的斜率为0时,显然 满足题意 满足题意
当AB的斜率不为0时,设 ,AB方程为 ,AB方程为 代入椭圆方程 代入椭圆方程 整理得 
则 


综上可知:恒有 .………………………………(文13分,理9分) .………………………………(文13分,理9分) 
| | |


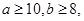 求数学成绩为优秀的人数比及格的人数少的概率.
求数学成绩为优秀的人数比及格的人数少的概率.
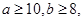 求数学成绩为优秀的人数比及格的人数少的概率.
求数学成绩为优秀的人数比及格的人数少的概率.